Analyse - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Analyse - Cours Première S

Analyse - Cours Première S

Forme canonique d'une fonction polynôme de degré 2

Trinôme et forme canonique

Une fonction polynome de second de degré "f" correpond à une somme de termes qui sont des constantes réelles, des multiples de la variable "x" (terme de degré 1) et des multiples de  la variable "x²" (terme de degré 2).

Cette fonction peut s'écrire sous la forme f(x) = ax² + bx + c
   
où:
- "a", "b" et "c" sont des réels (positifs ou négatif)
- "a" ne peut être nul sinon on obtient une fonction de la forme f(x) = bx + c qui corrrepond à un polynôme de degré 1 aussi appelé fonction affine

Toute fonction polynôme f(x) = ax² + bx + c  peut s'écrire sous une forme dite canonique qui prend la forme:

On peut montrer que

α = - b  
        2a
β = b² - 4ac
          4a

La forme canonique s'écrit donc également

On peut vérifier, qu'en développant cette expression, on obtient à nouveau la forme trinôme

Le discriminant

Le discrimant est un terme noté Δ (lettre grecque Delta) défini par l'expression:

En utilisant ce discriminant, la forme canonique d'une fonction polynôme de second degré s'écrit:

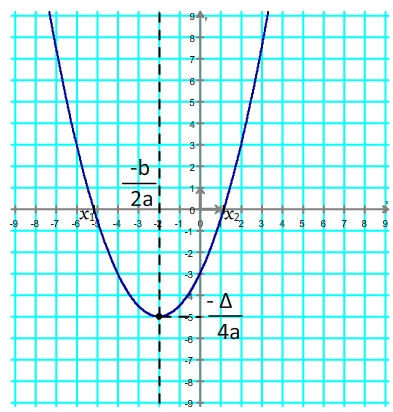
Forme canonique et caractéristiques de la parabole

La courbe représentative d'une fonction polynôme du second degré de formule f(x) = ax² + bx + c  est une parabole:
- dont le sommet a comme coordonnées
( -b ;  - Δ )
  2a    4a
- qui admet un axe de symétrie verticla d'équation
x = -b  
      2a
- qui est orientée vers le haut si "a" est positif
- qui  est orientées vers le bas si "a" est négatif

La forme canonique peut donc s'écrire:

où y_s est l'ordonnée du sommet de la parabole
     x_s est l'abscisse du sommet de la parabole

Comment trouver la forme canonique ?

Il est possible de trouver la forme canonique à partir du trinôme en suivant 3 méthode différentes

Méthode n°1

on utilise directement l'expression vue précédement :

Méthode n°2

Puisque la forme canonique peut s'écrire f(x) = a(x -x_s)² - y_s on peut chercher les coordonnées du sommet de la parabole (x_s; y_s)            

Pour cela on cherche à résoudre l'équation suivante:
ax² + bx + c = c
ax² + bx = 0
x(ax +b) = 0
cette solution admet deux solutions:
x = 0 et x = -b  
                   a
Les points de la parabole ayant ces abscisses sont symétriques l'un de l'autre, l'axe de symétrie se trouve au milieu de ces deux points, il a donc comme abscisse:
x_s = 1 . (0 +  -b )  soit x_s = -b
         2            a                  2a
Cette abscisse est aussi celle du sommet de la parabole dont l'ordonnée est y_s =f(x_s). La valeur ainsi obtenue correspond à
y_s =  - Δ
         2a
Méthode n°3

On cherche à factoriser la forme trinôme afin de faire apparaître la forme canonique

y = ax² + bx + c
y = a( x² + bx) + c
                 a
y = a( x² + bx +   b²  -   b² ) + c
                 a       4a²    4a²
y = a( x² + bx +   b²  ) -    b²  + c
                 a       4a²        4a²
y = a( x +  b )² -   b²  + c
                2a       4a
y = a( x +  b )² -   b²  - 4ac
                2a             4a
On retrouve bien la forme canonique