Analyse - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Première S
Analyse - Cours Première S
La fonction racine carrée
Définition
La fonction racine carrée est la fonction "f" qui à tout nombre de son ensemble de définition associe la racine carrée de ce nombre:
Ensemble de définition
La racine d'un nombre n'est défine que pour les nombres positifs, l'ensemble de définition de la fonction racine carrée est donc l'ensemble des nombres réels positifs qui correspond à l'intervalle [ 0 ; 
[
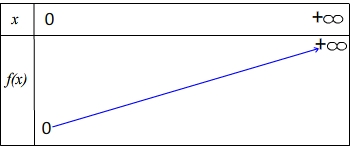
Variations
Soit "a" et "b" deux nombres de l'ensemble de définition de la fonction racine carrée tels que a < b
f(b) - f(a) =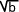 
- 
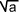
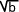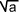= - x ( + )
+
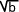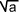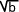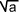
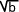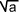= 2 - 2
+
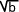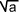
= b - a
+
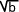Etant donné que b>a le numérateur (b-a) est toujours positif, tout comme le dénominateur qui est une somme de racines carrées donc f(b) - f(a) > 0 ce qui montre que la fonction racine carrée est strictement croissante sur son ensemble de définition.
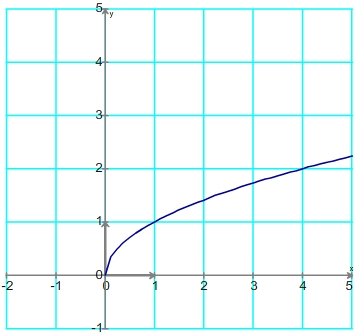
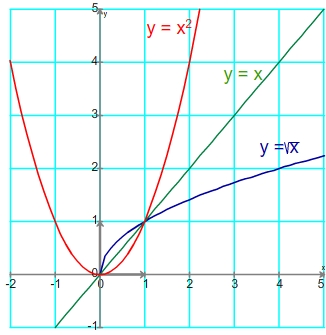
Comparaison des fonctions f(x) = et g(x) = x sur l'ensemble des réels positifs
f(x) - g(x) = - x
= .(1 - )
> 0
(1 - ) 
0 sur [0 ; 1]
(1 - ) 
0 sur [1 ;]
On en déduit donc que f(x) - g(x) est positif sur l'intervalle [0 ; 1] et négatif sur l'intervalle [1 ;]
Par conséquent:
Sur [0 ; 1] f(x) g(x) et x
Sur [1 ;] f(x) g(x) et x
Comparaison des fonctions g(x) = x et h(x) = x2 sur l'ensemble des réels positifs
g(x) - h(x) = x - x2
= x.(1 - x)
x 0
(1-x) 0 sur [0 ; 1]
(1-x) 0 sur [1 ;]
On en déduit donc que g(x) - h(x) est positif sur l'intervalle [0 ; 1] et négatif sur l'intervalle [1 ;]
Par conséquent:
Sur [0 ; 1] g(x) h(x) et x x2
Sur [1 ;] g(x) h(x) et x x2
Comparaison de , x et x2
On déduit des comparaisons précédentes que
x x2 et Sur [1 ;] x x2
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
