Analyse - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Première S
Analyse - Cours Première S
Fonction valeur absolue
Définition et ensemble de définition
La fonction valeur absolue est définie sur l'ensemble des nombres réels:
Sur l'intervalle ] 
; 0 ] est définie par la relation f(x) = -x
Sur l'intervalle [ 0 ;
[) est définie par la relation f(x) = x
La valeur d'un nombre réel correspond donc à ce même nombre s'il est positif et à son opposé s'il est négatif. En résumé cette fonction débarasse tout nombre de son signe négatif: toute image obtenue par cette fonction est donc un nombre positif.
Notation
On utilise une notation particulière pour l'image d'un nombre "x" par la fonction valeur absolue:
La valeur absolue d'un nombre réel "x" est notée |x| (x entre deux barres)
D'après la définition de la fonction valeur absolue:
|x| = x si x est positif et |x| = -x si x est négatif
Variations
Sur l'intervalle des nombres réels négatifs la fonction valeur absolue est définie par f(x) = -x, elle est donc assimilable à une fonction affine de forme ax + b pour laquelle a = -1 et b=0. Puisque son coefficient directeur est négatif cela implique qu'elle est décroissante sur cet intervalle.
Sur l'intervalle des nombres réels positifs la fonction valeur absolue est définie par f(x) = x, elle est donc assimilable à une fonction affine de forme ax + b pour laquelle a = 1 et b=0. Puisque son coefficient directeur est positif cela implique qu'elle est croissante sur cet intervalle.
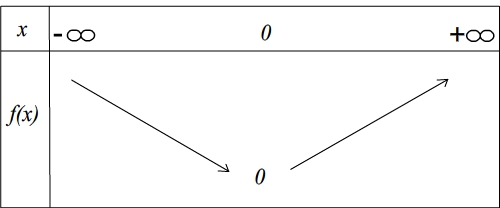
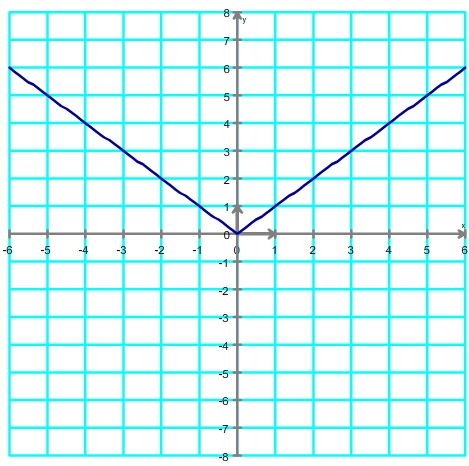
Représentation graphique
la fonction valeur absolue est paire puisque |-x| = |x| donc le graphique est symétrique par rapport à l'axe des ordonnées.
Valeur absolue et expression d'une distance
Si l'on considère un point M d'abscisse "x" sur un axe gradué d'origine O alors |x| (la valeur absolue de x) correspond à la distance entre le point O et le point M.
Plus généralement, si l'on considère deux point M et N d'un axe gradué d'abscisses repectives x et x' alors |x - x'| correspond à la distance qui sépare les points M et N.
Une distance est un nombre toujours positif, l'utilisation d'une valeur absolue pour l'exprimer est donc particulièrement adaptée puis que celle-ci fournit une valeur positive sans considération d'ordre (sans nécessité de faire la soustraction dans un sens particulier)
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
