Analyse - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Première S
Analyse - Cours Première S
Fonctions dérivées
Fonction dérivable
On dit qu'une fonction f est dérivable sur un intervalle I si elle dérivable en chaque point de cet intervalle.
Lorsqu'une fonction est dérivable sur un intervalle I on peut y définir une fonction dérivée notée f' qui à tout nombre de cet intervalle associe le nombre derivée par la fonction f
Fonction dérivée de la fonction constante
Cette fonction est définie sur l'ensemble des réels par f(x) = b où b est un réel
f'(x) =  f(x +h) - f(x)
f(x +h) - f(x)
h
f'(x) =  b-b
b-b
h
f'(x) =  0
0
h
f'(x) =  0
0
La dérivée de la fonction constante est donc nulle sur l'ensemble des réels:
Fonction dérivée d'une fonction affine
Cette fonction est définie sur l'ensemble des réels par f(x) = ax + b où a et b sont des réels
f'(x) =  a(x +h) +b - (a.x+b)
a(x +h) +b - (a.x+b)
h
f'(x) =  a.x+ a.h +b -a.x - b
a.x+ a.h +b -a.x - b
h
f'(x) =  a.h
a.h
h
f'(x) =  a
a
La dérivée d'une fonction affine est donc constante et égale au coefficient directeur sur l'ensemble des réels:
Fonction dérivée d'une fonction carré
Cette fonction est définie sur l'ensemble des réels par f(x) = x2
f'(x) =  f(x +h) - f(x)
f(x +h) - f(x)
h
f'(x) =  (x +h)2 - .x2
(x +h)2 - .x2
h
f'(x) =  x2+ 2x.h + h2 - x2
x2+ 2x.h + h2 - x2
h
f'(x) =  2x.h + h2
2x.h + h2
h
f'(x) =  2x + h
2x + h
f'(x) =2x
La dérivée d'une fonction carré correspond donc à une fonction linéaire d'équation y=2x sur l'ensemble des réels:
Fonction dérivée d'une fonction puissance
Cette fonction est définie sur l'ensemble des réels par f(x) = xn où est un entier.
On admet que la fonction dérivée est définie sur l'ensemble des réels par f'(x) = n.xn-1
Fonction dérivée de la fonction inverse
Cette fonction est définie sur l'intervalle ] ; 0[ U ]0 ;
; 0[ U ]0 ;  [ par f(x) = 1
[ par f(x) = 1
x
f'(x) =  f(x +h) - f(x)
f(x +h) - f(x)
h
1 - 1
f'(x) =  (x +h) x
(x +h) x
h
x - (x+h)
f'(x) =  (x +h).x x(x+h)
(x +h).x x(x+h)
h
x - (x+h)
f'(x) =  (x +h).x
(x +h).x
h
- h
f'(x) =  (x +h).x
(x +h).x
h
f'(x) =  - h
- h
h.x(x+h)
f'(x) =  - 1
- 1
x(x+h)
f'(x) =  - 1
- 1
x(x+0)
f'(x) =  - 1
- 1
x2
La dérivée d'une fonction inverse correspond donc à l'opposée du carrée de cette fonction, elle est également définie sur l'intervalle ] ; 0[ U ]0 ;
; 0[ U ]0 ;  [
[
x x2
Fonction dérivée de la fonction racine carrée
Cette fonction est définie sur l'ensemble des réels par f(x) = 
f'(x) =  f(x +h) - f(x)
f(x +h) - f(x)
h
f'(x) = 
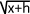 -
- 
h
f'(x) =  (
(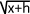 -
-  )(
)( 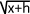 +
+  )
)
h.( 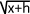 +
+  )
)
f'(x) =  x + h - x
x + h - x
h.( 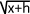 +
+  )
)
f'(x) =  h
h
h.( 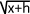 +
+  )
)
f'(x) =  1
1
( 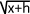 +
+  )
)
f'(x) =  1
1
( 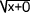 +
+  )
)
f'(x) =  1
1
(  +
+  )
)
f'(x) =  1
1
2.
La dérivée de la fonction racine carrée est donc égale à l'inverse du double de cette fonction, n'est pas définie sur l'ensemble des reéls mais sur l'intervalle ] ; 0[ U ]0 ;
; 0[ U ]0 ;  [.
[.
 alors f'(x)= 1
alors f'(x)= 1 2

Dérivée d'une combinaison linéaire de fonctions de référence
Si une fonction "f" est est définie comme le produit d'un réel "k" par une fonction de référence "u" alors la dérivée de cette fonction est le produit du réel "k" par la dérivée de la fonction "u"et leurs ensembles de définition sont les mêmes:
Si une fonction "f" est définie comme le produit de deux fonctions de référence "u" et "v" alors la dérivé de "f" est la somme des dérivées de "u" et "v". L'ensemble de définition de f' correspond à l'intersection des ensembles de définition de "u'" et "v'":
D'une manière générale, si une fonction "f" s'écrit sous la forme d'une combinaison linéaire de fonction "u" et "v" alors la dérivée de "f" s'écrit aussi sous forme d'une combinaison linéaire des dérivées de "u" et "v" et l'ensemble de définition de f' correspond à l'intersection des ensembles de définition de u' et v'.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
