Analyse - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Analyse - Cours Première S

Analyse - Cours Première S

Extremum d'une fonction

Définition d'un extremum

Un extremum est une valeur extrême, qui peut correspondre à un minimum ou à un maximum, prise par une valeur sur un intervalle donné.

Le maximum d'une fonction "f", définie sur un intervalle I, correspond à une valeur f(a)  ("a" appartenant à I) telle que pour tout nombre "x" de cet intervalle f(x)  f(a)

Le minimum d'une fonction "f" définie sur un intervalle I correspond à une valeur f(b), ("b" appartenant à I) telle que pour tout nombre "x" de cet intervalle f(x)  f(a)

Définition d'un extrememum local

Une fonction "f" définie sur un ensemble I admet un maximum local f(c) s'il existe un intervalle ouvert J, inclus dans I, sur lequel f(c) correspond à un maximum, c'est à dire tel que pour tout "x" de J, f(x)  f(c).

De même une fonction "f" définie sur un ensemble I admet un minimum local f(d) s'il existe un intervalle ouvert J, inclus dans I, sur lequel f(d) correspond à un minimum, c'est à dire tel que pour tout "x" de J, f(x)  f(c).

Exemples d'extremum et d'extremum local

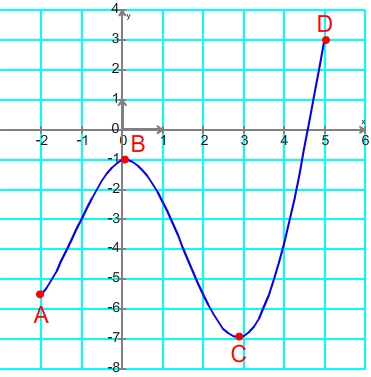
- Le maximum de la fonction "f" correpond à l'ordonnée du point D et sont minimum à l'ordonnée du point C

- L'abscisse du point C correpond également à un minimum local puisque qu'il le minimum, par exemple, sur l'intervalle ouvert ]1 ; 4[

- L'absisse du point B correpond à un maximum local puisqu'il est le maximum, par exemple, sur l'intervalle ouvert ]-1 ; 1[

Dérivée et extremum local

Si une fonction atteint un extremum local en un point "a" de son ensemble de définition alors la dérivée en ce point est nulle: f'(a) = 0

Pour trouver chaque extremum local d'une fonction il suffit de déterminer les points pour lesquelles sa dérivée s'annulle. Attention, cette condition est nécessaire mais n'est pas suffisante, il faut également qu'en ce point se produise un changement de variation (donc un changement de signe de la dérivée) sinon il ne correspond qu'à un palier de la fonction et non à un extremum.

Exemple:

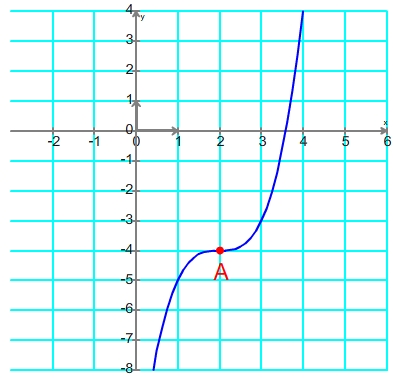
Cette courbe présente un palier horizontal au point A, donc la dérivée s'y annule mais sa variation reste la même avant et après ce point (elle est croissante) donc ce point n'est pas un extremum mais seulement un "palier"

Si la dérivée d'une fonction s'annule un point de son ensemble de définition et change de signe alors ce point correspond à un extremum local:
- si la dérivée est négative avant ce point (f décroissante) puis positive après (f croissante) alors il s'agit d'un minimum local.
- si la dérivée est positive avant ce point (f croissante) puis négative après (f décroissante) alors il s'agit d'un maximum local.