Analyse - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Première S
Analyse - Cours Première S
Signe d'une dérivée et sens de variation
Signe de la dérivée d'une fonction croissante
Soit "f", une fonction dérivable sur un intervalle I et croissante sur cet intervalle
Par définition, pour tout nombre a et b de cet intervalle tel que a 
b on a f(a) f(b)
On en déduit donc que si "a" et "a+h" appartiennent à l'intervalle I et que h est positif alors a a+h et:
f(a) f(a+h)
f(a+h) - f(a) 
0
f(a +h ) - f(a) 0
h
f(a +h) - f(a) 0
h
f'(a) 0
Signe de la dérivée d'une fonction décroissante
Soit "f", une fonction dérivable sur un intervalle I et décroissante sur cet intervalle
Par définition, pour tout nombre a et b de cet intervalle tel que a b on a f(a) f(b)
On en déduit donc que si "a" et "a+h" appartiennent à l'intervalle I et que h est positif alors a a+h et:
f(a) f(a+h)
f(a+h) - f(a) 0
f(a +h ) - f(a) 0
h
f(a +h) - f(a) 0
h
f'(a) 0
Si une fonction est décroissante et dérivable sur un intervalle alors sa dérivée est négative sur cet intervalle.
Signe de la dérivée d'une fonction constante
Soit "f", une fonction dérivable sur un intervalle I et constante sur cet intervalle
Par définition, pour tout nombre a et b de cet intervalle tel que a b on a f(a) = f(b)
On en déduit donc que si "a" et "a+h" appartiennent à l'intervalle I et que h est positif alors a a+h et:
f(a) = f(a+h)
f(a+h) - f(a) = 0
f(a +h ) - f(a) = 0
h
f(a +h) - f(a) = 0
h
f'(a) = 0
Remarque: la dérivée d'une fonction "f" en un point correspond au coefficient directeur de la tangente en ce point or celle-ci se confond localement avec la courbe de "f", les résultats obtenus sont donc conformes avec le fait qu'un coefficient directeur positif corresponde à une droite croissante, une coefficient négatif à une droite décroissante et un coefficient nul à une droite horizontale.
Signe de la dérivée et variations d'une fonction
On admet que le réciproque des résultats précédents est vérifiée. Si une fonction "f" est dériable sur un intervalle I alors:
Si sa dérivée est positive sur cet intervalle alors la fonction y est croissante.
Si sa dérivée est négative sur cet intervalle alors la focnction y est décroissante.
Si sa dérivée est nulle sur cet intervalle alors la fonction y est constante.
L'étude du signe de la dérivée d'une fonction permet donc d'établir les variations de cette dernière, elle est en particulier utile lorsque l'on n'a pas affaire à des fonction de références.
Exemple d'étude des variation d'une fonction à partir du signe de sa dérivée
Soit "f" la fonction définie sur l'ensemble des réels par f(x) = 2x3 - 6x2 +8
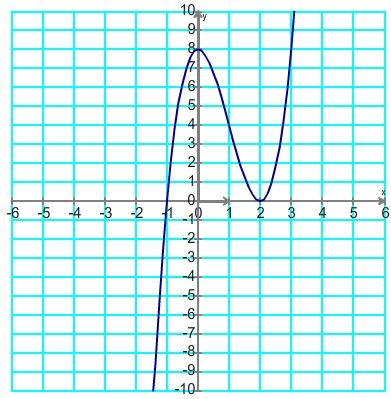
Sa fonction dérivée est:
f'(x) = 3.2x2 - 2.6x + 0
f'(x) = 6x2 - 12x
f'(x) = 6x.(x - 2)
Pour trouver le signe de f'(x) on peut établir un tableau:
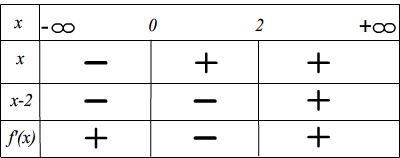
On déduit que:
- "f" est croissante sur ]
; 0] puisque sa dérivée est positive sur cet intervalle.
- "f" est décroissante sur [0 ; 2] puisque sa dérivée est négative sur cet intervalle.
- "f" est croissante sur [2 ; 
[ puisque sa dérivée est positive sur cet intervalle.
On peut donc compléter le tableau précédent
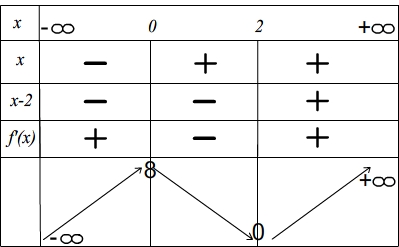
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
