Analyse - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Analyse - Cours Première S

Analyse - Cours Première S

Représentation graphique d'une suite

Représentation d'une suite générée par une formule directe

Une telle suite est définie à partir d'une formule de type u_n = f(n). Pour représenter "u", il suffit de tracer la courbe de la fonction "f" et de ne conserver que les points dont les abscisses sont des entiers naturels

Exemple: un = f(n) avec f(x) = 0.2x² +0,5x - 2

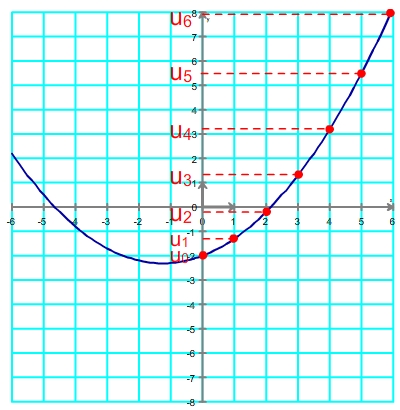
Si l'on ne conserve que les points correspondant à chaque terme on obtient la représentation finale

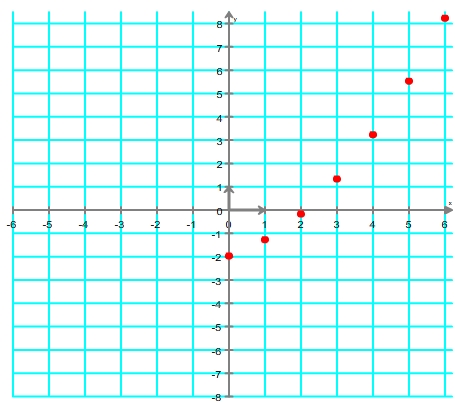
Représentation d'une suite définie par récurrence

Une telle suite est définie par une relation de type u_n+1 = f(u_n) et la donnée du terme initial.

Il existe deux possibilités pour représenter graphiquement une telle suite.

Soit calculer successivement les termes de différents rangs u₁ = f(u₀) puis u₂ = f(u₁), u₃ = f(u₂) etc puis reporter sur le graphe les points ainsi obtenus de coordonnées (0 ; u₀), (1 ; u₁), (2 ; u₂) etc

Soit utiliser la méthode de construction graphique suivante:

Etape 1: tracer la courbe représentant la fonction f
Etape 2: tracer la droite "d" d'équation y = x. Chaque point de cette droite possède une abscisse égale à son ordonnée
Etape 3: placer le point de coordonnées (u₀ ; 0)
Etape 4: chercher le point d'ordonnée f(u₀), on l'obtient en traçant une droite verticale passant par  (u₀ ; 0) et en cherchant son intersection avec la courbe "f". Ce point a comme ordonnée f(u₀), ce qui correspond à u₁ (puisque u₁ = f(u₀) )
Etape 5: projeter horizontalement le point de coordonnées (u₀ ; u₁) sur la droite "d" pour obtenir le point de coordonnées (u₁ ; u₁), une projection verticale permet ensuite de repporter le point (u₁ ; 0) sur l'axe des ordonnées.

Réaliser ensuite pour u₁ les même opérations que pour u₀ afin d'obtenir u₂ et ainsi de suite pour les termes de rang suivant.

Exemple:

La suite u est définie par:
- La relation de récurrence u_n = 0,5.U_n+1 +1
- Le terme initiale u₀ = 1

Etape 1: on trace la représentation de la fonction f(x) =0,5.x +1


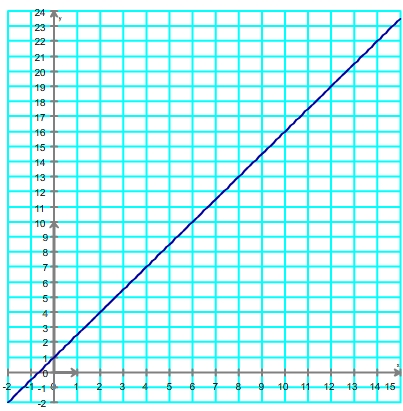
Etape 2: on trace la droite d'équation y = x


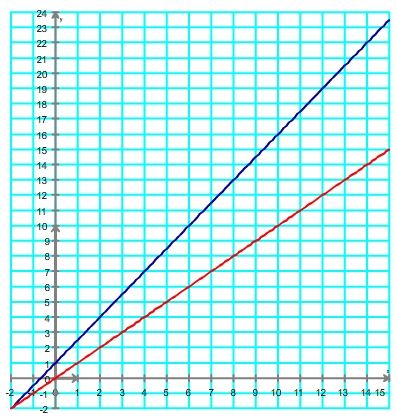
Etape 3: on place le point de  coordonnées (u₀ ; 0), à savoir (1 ; 0)


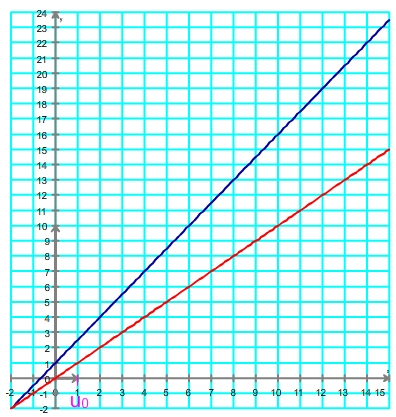
Etape 4: On obtient f(u₀), autrement dit u₁, en cherchant l'image de u₀ par f


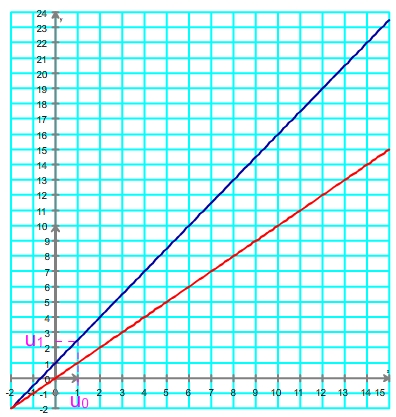
Etape 5:  on trace la droite horizontale d'ordonnée u₁ puis l'on cherche son intersection avec la droite d'équation y=x afin d'obtenir le point de coordonnées (u₁;u₁), ce qui permet ensuite de reporter le point (u₁;0) sur l'axe des ordonnées



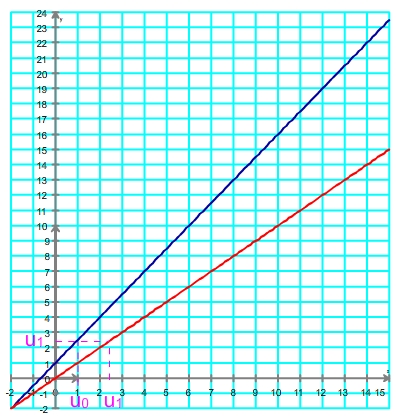
On reproduit les étapes 4 et 5 sur (u₁;0) afin d'obtenir afin  (u₂;0), on les répète sur (u₂;0) pour obtenir (u₃;0) etc

Obtention de u₂



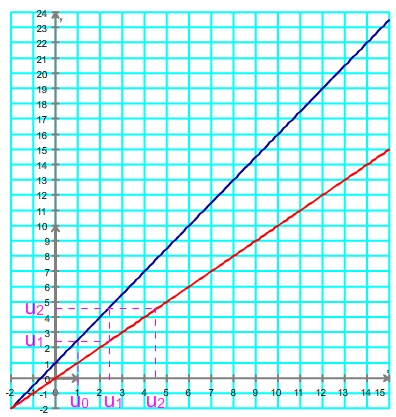
Obtention de u₃



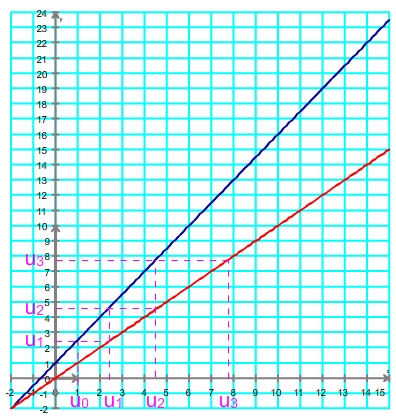
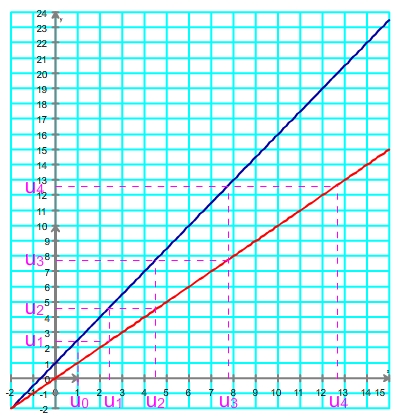
Obtention de u₄