Analyse - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Analyse - Cours Première S

Analyse - Cours Première S

Suites arithmétiques

Définition

Une suite arithmétique est une suite "u" définie par la donnée d'un terme initial u₀ et une relation de récurrence de la forme:

où "r" est un nombre réel (positif ou négatif ) appelé raison de la suite "u"

Pour définir une suite arithémique il suffit d'indiquer son terme initial ainsi que sa raison.
Une suite arithmétique est composée de termes qui s'accroissent d'une valeur "r" à chaque nouveau rang.

Exemples:
- Si u_n+1 = u_n + 2 et u₀ = 1 alors "u" est une suite arithémique de raison "2" avec u₁ = 1 + 2 = 3 ; u₂ = 3 + 2 = 5 ; u₃ = 5 - 2 = 7 etc

- Si u_n+1 = u_n - 3 et u₀ = 6 alors "u" est une suite arithmétique de raison "-3" avec u₁ = 6 - 3 = 3 ; u₂ = 3 - 3 = 0 ; u₃ = 0 - 3 = -3 etc

Remarque: l'ensemble des entiers naturels (0, 1, 2, 3, 4 etc) peut être décrit comme l'ensemble des termes d'une suite arithmétique de terme initial u₀ = 0 et de raison r = 1.

Expression d'une suite arithémique par une formule explicite

Toute suite arithmétique peut s'exprimer par grâce une fonction "f" avec f(n) =  u_n = n.r + u₀

Réciproquement, si une suite est définie par une fonction "f" de la forme f(x) = a.r +b alors il s'agit d'une suite arithmétique de raison r = a et de terme initial u₀ = b.

On peut vérifier qu'il eest possible de passer d'une forme à l'autre:
u_n+1 - u_n = f(n+1) - f(n)
u_n+1 - u_n = (n+1).r +u₀ - (n.r + u₀)
u_n+1 - u_n = n.r + r + u₀ -n.r -u₀
u_n+1 - u_n = n.r - n.r + u₀ - u₀ +r
u_n+1 - u_n = r
u_n+1 = u_n + r

Variations d'une suite arithmétique

Puisque u_n+1 = u_n + r on obtient u_n+1 - u_n = r on en déduit donc que:

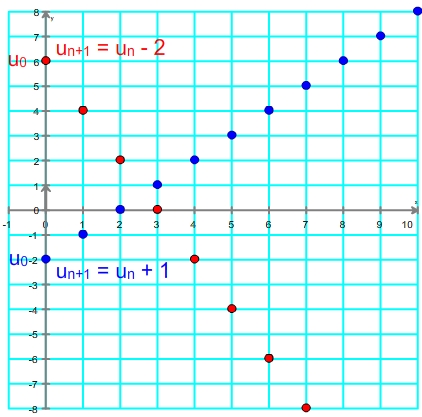
- si r est positive alors la suite est croissante
- si r est négative alors la suite est décroissante
- si r = 0 la suite est constante (égale à u₀)

Limites

Une suite arithmétique est toujours divergente:

Si la raison est positive alors la suite géométrique diverge vers
Si la raison est négative alors la suite géométrique diverge vers

Somme des termes d'une suite arithmétique

La somme "S" des N premiers termes d'une suite arithmétique (de u₀ à u_N-1) correspond à la moyenne du premier et du dernier terme multipliée par le nombre de termes ce qui peut se traduire par:

S = u₀ + u₁ + u₂ + u₃ ........ + u_N-1 =  ( u₀ + u_N-1) . N
                                                                    2
Si le premier terme est u₁ et le dernier u_N alors l'expression de cette somme devient:

S = u₁ + u₂ + u₃ ........ + u_N =  ( u₁ + u_N) . N
                                                       2
Si l'on additionne les termes de u₀ à u_N (soit N+1 terme) alors on obtient:

S = u₀ + u₁ + u₂ + u₃ ........ + u_N =  ( u₀ + u_N) . (N+1)
                                                               2