Géométrie - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Géométrie - Cours Première S

Géométrie - Cours Première S

Les angles orientés de vecteurs et leurs propriétés

Angle orienté de deux vecteurs identiques

L'angle orienté entre deux vecteurs identiques est un angle nul (à 2π près):

Angle orienté de deux vecteurs opposés

L'angle orienté entre deux vecteurs opposés est un angle plat qui vaut  π (180°) (à 2π près):

Relation de Chasle pour les angles orientés

Cette relation peut s'appliquer lorsque deux angles orientés font intervenir un même vecteur

Pour tous vecteurs , et quelconques, la somme de la mesure de l'angle entre le vecteur et le vecteur et de la mesure de l'anle entre le vecteur et le vecteur  est égale à l'angle entre le vecteur  et le vecteur :

 

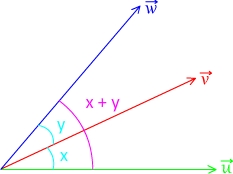
Comparaison des angles orientés ( ; ) et ( ; )

D'après la relation de Chasle on peut écrire que:

( ; ) + ( ; ) = ( ; )

( ; ) + ( ; ) = 0  (2π)

( ; ) = - ( ; ) (2π)

Lorsqu'on inverse l'ordre des vecteurs qui expriment un angle orienté on obtient un angle dont la mesure principale a même valeur mais un signe opposé.

Comparaison des angles orientés ( ; ) et (- ; -)

D'après la relation de Chasle on peut écrire que:

(- ; -) = (- ; ) + ( ; ) + ( ; -)

Or (- ; ) = π + (2π) et  ( ; -) π  (2π) (ce sont des angles plats) donc leur somme est π + π (2π) = 2π (2π) soit un angle nul.    

(- ; -) = ( ; ) + 0 (2π)

Pour tout angle ( ; ) on a la relation:  (- ; -) =  ( ; ) +  (2π)

La mesure d' angle orienté de deux vecteurs est donc égale à la mesure de l'angle des opposés de ces vecteurs.

Comparaison des angles orientés (- ; ) et ( ; )

D'après la relation de Chasle on peut écrire que:

(- ; ) = (- ; ) + ( ; )

(- ; ) =  π  (2π) + ( ; )