Géométrie - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie - Cours Première S
Géométrie - Cours Première S
Cosinus et sinus d'angles associés
Sinus et cosinus d'angles associés opposés
Soit "x" un angle et "-x" son angle associé
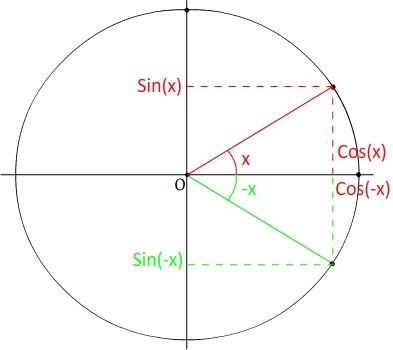
Cos (-x) = cos (x) et sin (-x) = - sin(x)
Le cosinus d'un angle a même valeur que cosinus de son angle opposé.
Le sinus d'un angle à une valeur opposée à celle du sinus de son angle opposé.
Sinus et cosinus d'angles associés complémentaires
Soit "x" un angle " x - π " son angle complémentaire
2
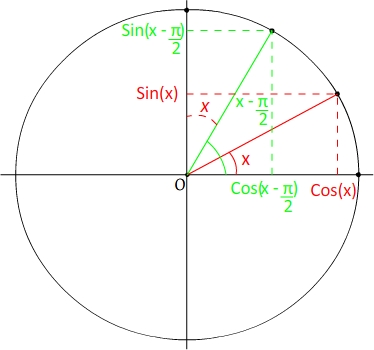
2 2
Le sinus d'un angle a donc la même valeur que le cosinus de son angle complémentaire.
Le cosinus d'un angle a donc la même valeur que le sinus de son angle complémentaire.
Sinus et cosinus d'angles associés supplémentaires
Soit "x" un angle et "π - x" son angles supplémentaire.
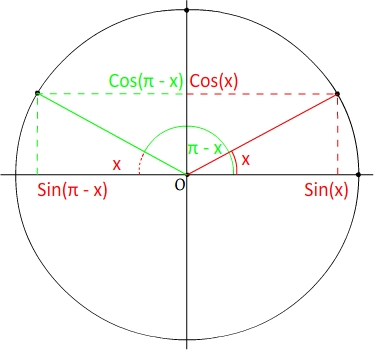
Le cosinus d'un angle a donc une valeur opposée à celle du cosinus de son angle supplémentaire.
Le sinus d'un angle a donc la même valeur que celle du sinus de son angle supplémentaire.
Sinus et cosinus d'angles anticomplémentaires
Soit "x" un angle et" x + π " son angle anticomplémentaire.
2
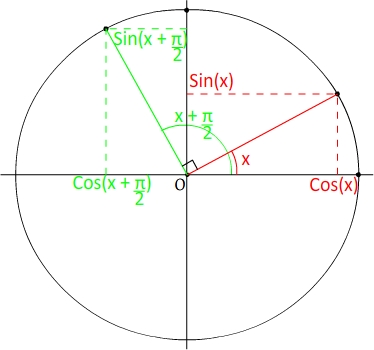
2 2
Le sinus d'un angle est donc égal à l'opposé du cosinus de son angle anticomplémentaire.
Le cosinus d'un angle est égal au sinus de son angle anticomplémentaire.
Résoudre une équation du type sin(x) = sin(a)
Les résultats obtenus en comparant les cosinus et sinus d'angles associés permettent de proposer des solutions à certaines équations faisant intervenir des sinus et des cosinus. En particulier il possible de résoudre l'équation suivante:
Sin(x) = sin(a)
où x est l'inconnue et "a" une constante réelle
Première solution x = a
Cette solution s'acompagne également de tous les angles égaux à
x = a + k2π avec k un entier relatif
Par ailleur le sinus d'un angle à la même valeur que le sinus de son angle supplémentaire, une autre solution est donc:
x = π - a
Par ailleurs cet angle est équivalent a tous ceux obtenu en ajoutant un multiple de 2π on peut donc inclure aussi dans les solutions:
x = π - a + k2π ou k est un entier relatif
L'équation sin(x) = sin(a) comprend donc une infinité de solutions correspondant aux réels tels que
x = a + k2π ou x = π - a + k2π où "k" est entier naturel
Résoudre une équation du type cos(x) = cos(a)
Les comparaisons de sinus et cosinus d'angles associés contribuent à la résolution de l'équation suivante:
cos(x) = cos(a)
où x est l'inconnue et "a" une constante réelle
Première solution x = a
Cette solution s'acompagne également de tous les angles égaux à
x = a + k2π avec k un entier relatif
Par ailleur le cosinus d'un angle à la même valeur que le cosinus de son angle opposé, une autre solution possible est donc:
x = - a
Par ailleurs cet angle est équivalent a tous ceux obtenu en ajoutant un multiple de 2π on peut donc ajouter également les solutions suivantes:
x = - a + k2π ou k est un entier relatif
L'équation cos(x) = cos(a) comprend donc une infinité de solutions correspondant aux réels tels que
x = a + k2π ou x = π - a + k2π où "k" est entier naturel
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
