Géométrie - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Géométrie - Cours Première S

Géométrie - Cours Première S

Equation d'un cercle

Etablir l'équation d'un cercle à partir de son diamètre

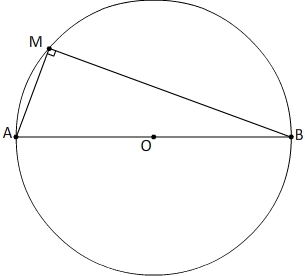
Si AB est le diamètre d'un cercle de centre O alors celui-ci possède une propriété qui peut être exploitée pour établir son équation:

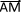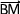Si un point M(x;y) appartient au cerle alors (AM) est perpendiculaire à (BM) autrement dit les vecteurs et  sont orthogonaux.

Le produit scalaire de ces deux vecteur est donc nul: 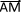. 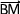= 0

Or ce produit scalaire peut également être exprimé à partir des coordonnées des vecteur:

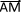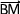. = x_AM.x_BM + y_AM.y_BM
            = (x-xA).(x-xB) + (y-yA).(y-yB)

Puisque le produit scalaire est nul on obtient donc l'équation du cercle:

(x-xA).(x-xB) + (y-yA).(y-yB) = 0

Etablir l'équation d'un cercle à partir de son rayon
 
Le produit scalaire précédent (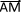.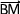) peut être développé:

. = ( + ).( + )
             = . + . +. + .
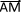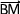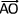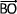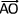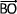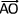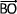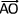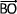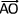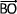             = (+). + . + ²

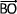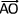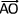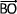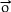Puisque O est le milieu du segment [AB] = - donc + =   et 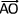. 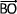= - 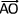. 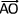= - AO² on obtient donc;

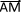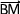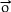. = .  - AO² +   ²
            = - AO² +   ²

Puisque le produit scalaire 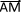. 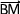est nul ont obtient on trouve l'équation:

² - AO² = 0   

AO peut être noté R puisqu'il correspond au rayon donc:

(x-x_O)² + (y-y_O)² + R = 0