Géométrie - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Géométrie - Cours Première S

Géométrie - Cours Première S

Formules d'addition et de duplication des sinus et cosinus

Formules d'addition des sinus et cosinus

Ces formules permettent d'exprimer les cosinus et les sinus pour des sommes ou des différences.

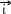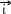On considère des vecteurs unitaires (dont la norme est 1) situés dans le cercle trigonométrique: tel (,) = b et tel que (,) = a

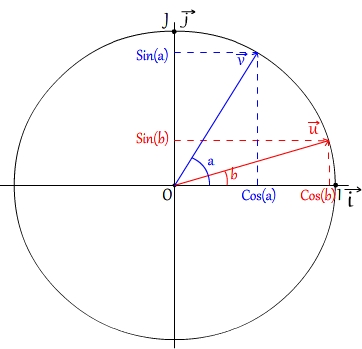
Dans cercle les coordonnées des vecteurs sont (cos(a);sin(a)) et (cos(b);sin(b))

Le produit scalaire de ces deux vecteurs peut être exprimé d'une part à l'aide des norme et des angles:

. = ||||.||||.cos(a-b)
         = 1 . 1 . cos(a-b)
         = cos(a-b)

On peut aussi exprimer ce produit scalaire en utilisant les coordonnées des deux vecteurs:

. = cos(b).cos(a) + sin(b).sin(a)

Si dans la formule précédent on remplace "b" par "-b", on obtient une nouvelle égalité:

cos(a-(-b)) = cos(a).cos(-b) + sin(a).sin(-b)

cos(a+b) = cos(a).cos(b) - sin(a).sin(b)  ( car cos(-b) = cos(b) et sin(-b) = -sin(b) )

On considère maintenant cos(π/2 -(a-b)):

D'une part cos(π/2 -(a-b)) = sin(a-b) (car sin(cos(π/2 -x) = sin(x))

D'autre part cos(π/2 -(a-b) = cos(π/2 -a + b) on donc considérer que l'angle est la somme de π/2 - a et de b, on peut appliquer la formule démontrée précédemment.
           
cos(π/2 -a + b) = cos(π/2 -a).cos(b) - sin(π/2 -a).sin(b)
                        = sin(a).cos(b) - cos(a).sin(b)

Si dans la formule précédente "b" est remplacé par "-b" on obtient une nouvelle égalité:

sin(a- (-b)) = sin(a).cos(-b) - cos(a).sin(-b)
sin(a + b) = sin(a).cos(b) - cos(a).(-sin(b))

Formules de duplication des sinus et cosinus

Si dans l'égalité cos(a+b) = cos(a).cos(b) - sin(a).sin(b) on remplace "b" par "a", on obtient:

cos(a+a) = cos(a).cos(a) - sin(a).sin(a)
cos(2a) = cos²(a) - sin²(a)

Par ailleurs cos²(a) + sin²(a) = 1 donc cos²(a) = 1 - sin²(a) et sin²(a) = 1 - cos²(a) ce qui permet d'aboutir aux égalités:

Cos(2a) = cos²(a) -(1 - cos²(a))
              = 2cos²(a) -1

ou
Cos(2a) = 1 - sin²(a) - sin²(a)
              = 1 - 2sin²(a)

Si l'on remplace maintenant "b" par "a" dans la formule sin(a+b) = sin(a).cos(b) + cos(a).sin(b) on obtient:

sin(a+a) = sin(a).cos(a) + cos(a).sin(a)
sin(2a) = 2.sin(a).cos(b)