Géométrie - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Géométrie - Cours Première S

Géométrie - Cours Première S

Le produit scalaire et les différentes méthodes pour le calculer

Le produit scalaire est une opération qui associe à deux vecteurs , du plan, un réel (positif ou négatif). Il existe  différentes méthodes qui permettent de le calculer.

Le produit scalaire d'un vecteur par un vecteur se note .  (ce qui se lit "u scalaire v")

Calculer un produit scalaire à partir des normes et d'un angle

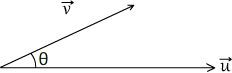
Le produit scalaire de deux vecteurs et  de normes respectives |||| et |||| faisant entre eux un angle (, ) = θ (lettre grecque thêta) peut être calculé en faisant le produit de leurs normes et du cosinus de leur angle, soit:

Cette expression implique que:
- le produit scalaire n'est nul que si l'un des vecteurs est nul ou si les vecteurs sont perpendiculaires ( θ =   π  (2π) )
                                                                                                                                                                               2
- le produit scalaire est positif lorque l'angle est aigu et négatif lorsque l'angle est obtu
- le produit scalaire d'un vecteur par lui-même est égal à .  = ||||.||||.cos(0) = ||||². Un tel produit scalaire est en général noté .  = ²    

Calculer un produit scalaire avec une projection orthogonale

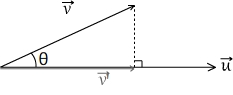
Dans l'expression précédente du produit scalaire, le produit ||||.cos(θ), correspond à la projection orthogonale du vecteur  sur le vecteur . Si l'on note ' le vecteur résultant de cette projection alors le produit scalaire peut se calculer à partir de l'expression suivante:

 

Calculer un produit scalaire uniquement avec des normes

|| + ||² = ² + ² +2 .

On peut donc en déduire que :

|| - ||² = ² + ² -2 .

On également en déduire que:

Calculer un produit scalaire dans un repère orthonormé

D'après les relations du paragraphe précédent:

         = 0,5.[ (x_u +x_v)² + (y_u + y_v)² - (x_u² + y_u²) - (x_v² +y_v²)]
         = 0,5.[ x_u² + x_v² + 2x_ux_v + y_u² + y_v² + 2y_uy_v - x_u² - y_u² - x_v2 - y_v2]
         = 0,5.[ + 2x_ux_v + 2y_uy_{v ]}
         = x_ux_v + y_uyv

Le produit scalaire d'un vecteur (x ; y) avec un vecteur  (x';y') peut donc être calculé en utilisant la relation suivante: