Géométrie - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie - Cours Première S
Géométrie - Cours Première S
Application du produit scalaire au calcul d'angles: le théorème d'Al-Kashi
Le théorème d'Al-Kashi est une généralisation du théorème de pythagore qui s'applique dans les tous les triangles (et pas seulement les triangles rectangle) où il permet de calculer la longueur des différents cotés mais aussi la valeur des angle de chaque sommet.
Il est possible démontrer ce théorème en utilisant les produits scalaires et leurs propriétés.
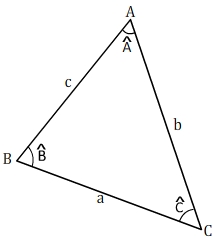
On considère un triangle quelconque ABC dans lequel, pour simplifier:
- Le coté BC (opposé au sommet A) a une longueur notée "a"
- Le coté AB (opposé au sommet C) a une longueur notée "c"
- Le coté AC (opposé au sommet B) a une longueur notée "b"
- L'angle B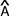 C est noté
C est noté 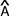
- L'angle C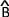 A est noté
A est noté 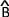
- L'angle A B est noté
B est noté 
Le produit scalaire du vecteur  par lui même est égal à:
par lui même est égal à:
 .
. =
=  2
2
= BC2
= a2
On peut également exprimer  comme la somme du vecteur
comme la somme du vecteur 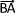 et du vecteur
et du vecteur  :
:
 .
. = (
= (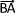 +
+  ).(
).(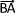 +
+  )
)
= (- +
+  ).(-
).(- +
+  )
)
= ( -
-  ).(
).( -
-  )
)
= ( -
-  )2
)2
On reconnait une identité remarquable de la forme ( -
-  )2 =
)2 =  2 -2
2 -2 .
. +
+  2
2
 .
. =
=  2 +
2 +  2 -2
2 -2 .
.
= AC2+ AB2 - 2 .
.
= b2 + c2 -2bc.cos(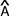 )
)
On obtient donc finalement l'égalité:
a2 = b2 + c2 -2bc.cos(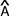 )
)
Cette relation permet de calculer la longueur "a" si "b", "c" et l'angle 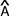 sont connus mais elle permet également d'isoler et de calculer cos(
sont connus mais elle permet également d'isoler et de calculer cos(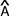 ): cos(
): cos(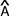 ) = (b2 + c2 - a2 )/(2bc) ce permet d'en déduire la mesure de l'angle
) = (b2 + c2 - a2 )/(2bc) ce permet d'en déduire la mesure de l'angle 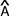 .
.
Cette relation peut se généralise donc d'après le théorème d'Al-Kashi:
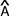 )
)b2 = a2 + c2 -2ac.cos(
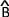 )
)c2 = b2 + a2 -2ba.cos(
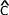 )
)
Le carré du coté opposé à un sommet du triangle est la somme du carré du premier coté adjacent et du carré du deuxième coté adjacent auquel on retranche le produit du premier coté adjacent par le deuxième coté adjacent par le cosinus de l'angle de ce sommet.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
