Géométrie - Cours Première S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Géométrie - Cours Première S

Géométrie - Cours Première S

Application du produit scalaire au calcul de longueurs: le théorème de la médiane

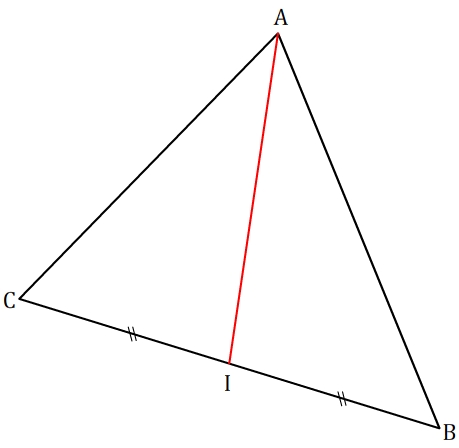
Rappel de la définition de la médiane: dans un triangle, la médiane issue d'un sommet est le segment qui joint ce sommet au milieu du coté oposé.

Le théorème de la médiane permet de caluler la longueur d'une médiane lorsqu'on connait celle des cotés.

Il est possible de démontrer ce théorème en faisant appel au produit scalaire et ses propriété

On considère un triangle ABC, et l'une de ses médianes issue du sommet "A" et passant par le milieu "I" du coté BC

Si l'on considère le produit scalaire du vecteur  par lui même:

. = ²
          = BC²

Le vecteur peut également être exprimé comme la somme du vecteur 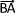 et et vecteur  on a donc également l'égalité suivante:

. = ( + ).( + )
          = (- + ).(- + )
          =( - ).( - )

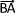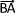Il s'agit d'une identité remarquable ( - )² = ² -2.+ ²

. = ² + ² -2.
          = AC²+ AB² - 2.

Le vecteur  peut être exprimé comme la somme 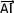 + 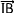et le vecteur   peut être exprimer comme la somme  +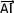

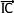
. = AC²+ AB² - 2( + ).( + )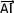

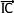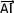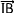Puisque le point "I" est le milieu du segment [AB]:  = -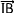

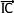
. = AC²+ AB² - 2( + ).( - )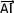

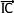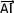Le dernier terme correpsond à une identité remarquable du type ( + ).( - ) = ² - ²

. =AC²+ AB² - 2(AI² -IC²)  

Avec IC = 0,5.BC  (IC est la moitié de BC)

. = AC²+ AB² - 2(AI² -(0,5BC)²)  
          = AC²+ AB² - 2(AI² - 0,25.BC²)
          = AC²+ AB² - 2(AI² - 0,25.BC²)
          = AC²+ AB² - 2AI² + 0,5.BC² 

D'après la première égalité  . = BC² donc:  
BC² = AC²+ AB² - 2AI² + 0,5.BC² 
BC² - 0,5.BC² +  2AI²  = AC²+ AB²   
0,5.BC² +  2AI²  = AC²+ AB²

On aboutit au théorème de la médiane
Dans un triangle quelconque ABC où I est le milieu de BC alors la longueur AI de la médiane issue de A resepecte l'égalité  suivante:

Remarques:

- Cette expression permet facilement d'en déduire la longueur AI de la médiane ( il s'agit de la racine carrée de  0,5.AC²+ 0,5.AB²- 0,25  BC²) mais cette formulation est simple à retenir.
 
- Ce résultats peut être adapé aux médiane du triangle, d'une manière générale:

la somme de la moitité du carré du coté opposé et du double du carré de la médiane est égale à la somme du  carrée du premier coté adjacent et du carré du deuxième coté adjacent.