Statistiques - probabilités - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques - probabilités - Cours Première S
Statistiques - probabilités - Cours Première S
Espérance, variance et écart type
L'espérance
Définition: Si X est une variable muni d'une loi de probabilité p dont les différentes valeurs prises sont x1, x2, x3, x4....xk alors on peut définir une grandeur appelée "espérance", notée E telle que:
E(X) = x1.p(X= x1) + x2.p(X= x2) + x3.p(X= x3) + x4.p(X= x4) ........ + xk.p(X= xk)
On peut également noter cette formule:
E(X) = 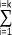 xi.p(X= xi)
xi.p(X= xi)
On simplifie souvent en remplaçant la notation p(X= xi) par pi ce qui donne:
E(X) = 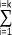 xi.pi
xi.pi
Si l'expérience aléatoire est répétée un grand nombre de fois alors la fréquence de chaque valeur obtenue tend à se rapprocher de plus en plus de la probabilité qui lui est associée et dans cas la moyenne (qui peut s'exprimer  =
= 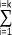 xi.fi tend également à se rappocher et à se confondre avec l'espérance.
xi.fi tend également à se rappocher et à se confondre avec l'espérance.
On peut donc interpréter l'espérance comme la valeur moyenne que l'on peut "espérer" obtenir en répétant une exprérience aléatoire un nombre de fois assez grand.
Puisque l'on peut définir une grandeur (l'espérance) comparable à la moyenne on peut également définir des grandeurs qui en dérivent telles que la variance et l'écart type.
La variance
La variance V d'une variable alétoire X est définie par la relation suivante:
V(X) = (x1 - E(X))2 . p1 + (x2 - E(X))2 . p2 + (x3 - E(X))2 . p3 + (x4 - E(X))2 . p4 ......... + (xk - E(X))2 . pk
Ce qui donne en écriture condensée:
V(X) = 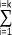 (xi - E(x))2.pi
(xi - E(x))2.pi
Tout comme la variance statistique, l'expression de cette variance peut être simplifiée et s'écrire:
V(X) = [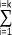 xi2.pi] - (E(x))2
xi2.pi] - (E(x))2
L'écart type
A la différence des statistique l'écart type des probabilité se note σ (lettre grecque sigma) mais sa définition reste la même: il s'agit de la racine carrée de la variance:
σ= 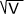
Transformation affine d'une variable aléatoire
Si X est une variable aléatoire, a et b deux réels alors on peut définir une nouvelle fonction aléatoire X' telle que X'=aX +b (on dit que X' est le résultat de la transformation affine de X).
Dans ce cas:
E(aX + b) = a.E(x) + b
V(aX +b) = a2.V(x)
σ(aX+b) = |a|.σ(X)
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
