Statistiques - probabilités - Cours Première S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques - probabilités - Cours Première S
Statistiques - probabilités - Cours Première S
Schéma de bernoulli, loi binomiale
Schéma de Bernouilli
Définitions
Un schéma de Bernoulli est l'expérience obtenue en répétant "n" fois des épreuves de Bernoulli identiques entre elles et indépendantes.
Loi binomiale
Si X est une variable aléatoire correspondant au nombre succès obtenus lors d'un schéma de Bernoulli avec "n" répétions d'épreuves de Bernoulli dont chacune est caractérisée par une probabilité "p" de succès alors la loi de probabilité associée à cette variable est appelée loi binomiale de paramètre "p" et "n", on la note en général B(n;p).
Coefficient binomial
Pour chaque épreuve de Bernouli de paramètre "n" et "p" on peut définir des coefficients binomiaux. Ils sont notés sous la forme 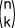 (ce qui se lit k parmi n) et correpond au nombre de branches de l'arbre prondéré qui permet d'obtenir "k" succès lors d'un schéma de Bernoulli répétant "n" fois la même épreuve.
(ce qui se lit k parmi n) et correpond au nombre de branches de l'arbre prondéré qui permet d'obtenir "k" succès lors d'un schéma de Bernoulli répétant "n" fois la même épreuve.
Expression de la loi binomiale
La probabilité d'obtenir un nombre de "k" succès par une loi binomiale de paramètres "p" et "n" peut être exprimée à l'aide d'une formule déduite de l'arbre pondérée.
Chaque chemin menant à "k" succès" est constitué de "k" branches "succès" (probabilité p) et de "n-k" branches "échec" (probabilité 1-p). Tous ces chemins possèdent donc la même probabilité obtenue en multipliant la probabilité des différente branches soit: pk.(1-p)n-k
La probabilité totale d'obtenir "k" succès s'obtient dont en aditionnant les probabilité de toutes les branches à "k" succès ce qui peut être exprimé par le le coefficient binomial 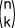 . Au final l'espression de la loi binomiale est:
. Au final l'espression de la loi binomiale est:
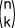 . pk.(1-p)n-k
. pk.(1-p)n-k
Espérance et variance d'une loi binomiale
Si une variable aléatoire X suit une loi binomiale B(n;p) alors:
Sa variance est V(X) = n.p.(1-p)
Remarque: la variance et l'espérance sont "n" fois plus élevées que celles de la loi de Bernoulli définie à partir de la même épreuve.
Exemple de schéma de Bernoulli et de loi binomiale
Lorsqu'on jette une pièce non équilibrée on peut définir comme succès l'obtention de "face" et comme échec l'obtention de "pile". Il s'agit d'une épreuve de Bernoulli donc le fait de répéter 3 fois un lancer de pièce constitue un schéma de Bernoulli et la loi binomial indique la probabilité d'obtenir trois fois de suite "face". Si cette dernière est obtenue avec une probabilité de 0,6 et "pile avec 0,4 alors cette expérience est décrite par la loi de binomiale B(3;0,6)
Pour exprimer la loi binomiale on a besoin de déterminer la valeurs des coefficients binomiaux que l'on peut trouver à partir de l'arbre pondérée ou à partir de la méthode décrite par le cours sur les "propriétés des coefficients binomiaux".
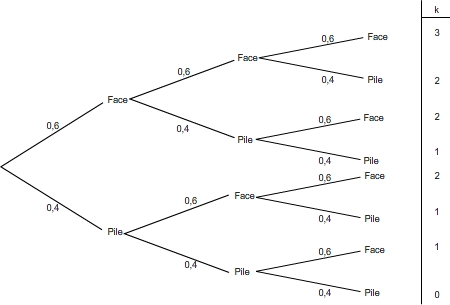
La loi binomiale s'exprime sous la forme: P(X=k) = 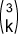 . 0,6k.(1-0,6)3-k
. 0,6k.(1-0,6)3-k
On obtient alors:
Si k = 0 alors 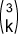 = 1 et P(X=0) = 1. 0,60.(1-0,6)3-0 = 1.1.(0,4)3 = 0,064
= 1 et P(X=0) = 1. 0,60.(1-0,6)3-0 = 1.1.(0,4)3 = 0,064
Si k = 1 alors 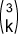 = 3 et P(X=1) = 3. 0,61.(1-0,6)3-1 = 3.0,6.(0,4)2= 0,288
= 3 et P(X=1) = 3. 0,61.(1-0,6)3-1 = 3.0,6.(0,4)2= 0,288
Si k = 2 alors 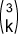 = 3 et P(X=2) = 3. 0,62.(1-0,6)3-2 = 3. 0,62.(0,4)1 = 0,432
= 3 et P(X=2) = 3. 0,62.(1-0,6)3-2 = 3. 0,62.(0,4)1 = 0,432
Si k = 3 alors 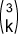 = 1 et P(X=3) = 1. 0,63.(1-0,6)3-3 = 1. 0,63.(0,4)0 = 0,216
= 1 et P(X=3) = 1. 0,63.(1-0,6)3-3 = 1. 0,63.(0,4)0 = 0,216
L'espérance est E(X) = n.p
= 3.0,6
= 1,8
La variance est V(X) = n.p.(1-p)
= 3.0,6.(1-0,6)
= 0,72
L'écart type est de 0,85
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
