Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Comportement à l'infini de la suite (qn)
Le comportement à l'inifini d'une suite géométrique de forme un = qn dépend de la valeur sa raison, le nombre réel "q", selon cette dernière la suite pourra être convergente ou divergente.
Suite géométrique avec q > 1
Si la raison est supérieure à "1" on peut démontrer que la suite géométrique diverge vers 
mais pour cela on a besoin de l'inégalité de Bernoulli:
1 + n.a
Si q > 1 alors il peut s'écrire sous la forme q = 1 + a où "a" est un réel positif donc, d'après l'inégalité de bernoulli:
1 + n.a
or la suite 1 + n.a diverge vers , puisque qn lui est supérieur cette suite géométrique diverge aussi vers l'infini
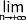(qn) =
Suite géométrique avec q = 1
Dans ce cas la suite géométrique est constante et égale à "1" donc
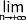(qn) = 1
Suite géométrique avec -1 < q < 1
Puisque -1 < q < 1 alors |q|<1 et 1 > 1
|q|
Puisque le terme 1 est supérieur à 1 alors une suite géométrique de raison ( 1 )n = 1 a pour limite .
|q| |q| |q|n
Son inverse (à savoir |q|n tend donc vers 0 de même que qn.
Pour tout réel q tel que -1 < q < 1 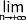(qn) = 0
Suite géométrique avec q = 1
Dans ce cas les valeurs prises par la suite géométrique sont alternativement "1" lorsque "n" est pair et "-1" lorsque "n" est impair, la suite diverge sans avoir de limite infinie.
Suite géométrique avec q < -1
Si la raison "q" est inférieur à -1 ses termes sont égaux à |q|n pour les valeurs paires de "n" et à -|q|n pour les valeurs impaires de "n". Or |q|n tend vers et -|q|n tend vers 
ce qui signifie que qn n'est pas bornée, c'est donc une suite divergente. Par ailleurs, puisqu'elle alterne les valeurs positives et négatives, elle n'a pas de limite.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
