Analyse - Cours Terminale S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Analyse - Cours Terminale S

Limites et comparaisons

Comparaison de suites convergentes

Si à partir d'un certain rang une suite u_n reste inférieure à une suite v_n et que ces deux suites sont convergentes avec 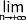limite lorsque n tend vers plus l'inifini u_n= l₁ et 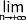v_n= l₂ alors la limite de la suite u_n est inférieure à celle de suite v_n : l₁ < l₂

Remarque: si les suites sont inférieures ou égales leur limite sont aussi inférieures ou égales.

Théorème des gendarmes

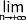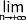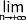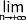Si trois suites u_n, v_n et w_n sont telles qu'à partir d'un certain rang v_n soit encadrée par u_n et w_n ( c'est à dire u_n inférieur ou égal v_n w_n ) et si u_n et w_n sont convergentes avec la même limite "l" ( limite lorsque n tend vers plus l'inifini u_n= w_n= l ) alors la suite v_n est aussi convergente et sa limite est la même que celle de u_n et v_n : ( u_n= v_n = 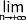w_n= l )

Exemple

Soit trois suites:
u_n = -1
n²
v_n = cos (n)
   n²
w_n = 1
n²
Puisque 1 inférieur ou égal cos(n) 1 alors pour tout n: 1 cos(n) 1
n² n²    n²
donc u_n v_n w_n

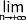or limite lorsque n tend vers plus l'inifini 1 = 0 et 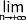- 1 = 0
  n²     n²
La suite u_n est donc convergente et admet la même limite que u_n et w_n : 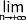v_n = 0

Comparaison de suites qui divergent vers l'infini

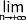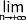Si deux suites u_n et v_n sont telles qu'à partir d'un certain rang u_n est inférieure ou égale à v_n et que la limite de u_n est plus l'infini ( limite lorsque n tend vers plus l'inifini u_n= ) alors la limite de v_nest aussi plus l'infini: v_n=

En effets si 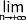u_n= alors alors pour tout réel "a", il existe un rang n₀ à partir duquel tous les termes de la suite appartiennent à l'intervalle ] a ; [ puisque u_n inférieur ou égal v_n on a également a u_n v_n donc a v_n ce qui implique que les termes de v_n au delà du rang n₀ appartiennet aussi à l'intervalle ] a ; plus l'infini [ . 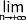Donc pour tout réel "a" il existe donc aussi un rang à partir duquel tous les termes de la suite vn appartiennent à ] a ; [ ce qui signifie que limite lorsque n tend vers plus l'inifini v_n=

De même si deux suites u_n et v_n sont telles qu'à partir d'un certain rang u_n est supérieure ou égale à v_n et que la limite de u_n est moins l'infini ( 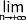u_n= plus l'infini ) alors la limite de v_nest aussi moinsl'infini: 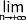v_n=

Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :

Je suis en *

Nom *

Prénom *

Email *

Téléphone

Code postal *

Glisser pour déverrouiller le formulaire

$amazon livre apprendre math$
Livre référence pour apprendre les mathématiques