Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Asymptote parallèle à l'un des axes de coordonnées
Asymtoptes horizontales
Si une fonction f(x) admet une limite finie "b" en  alors on dit qu'elle possède une asymptote en
alors on dit qu'elle possède une asymptote en  , cette asymtote est une droite horizontale d'équation y = b
, cette asymtote est une droite horizontale d'équation y = b
L'asymptote de f(x) en  est la droite avec laquelle la représentation de la fonction tend à se confondre en
est la droite avec laquelle la représentation de la fonction tend à se confondre en 
De même si une fonction f(x) admet une limite finie "c" en  alors elle possède une asymptote en
alors elle possède une asymptote en  , il s'agit de la droite horizontale d'équation y = c
, il s'agit de la droite horizontale d'équation y = c
Exemple
Si f(x) = 1 + 3
x
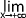 f(x) = 3 et
f(x) = 3 et 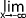 f(x) = 3
f(x) = 3
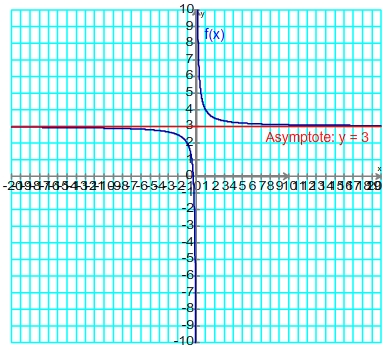
La fonction f(x) admet donc une asymptote commune en  et en
et en  d'équation y = 3
d'équation y = 3
Asymptote verticale
Si une fonction f(x) possède une limite infinie (  ou
ou  ) en un point "a" alors elle admet une asymptote qui est une droite verticale d'équation x = a.
) en un point "a" alors elle admet une asymptote qui est une droite verticale d'équation x = a.
Remarque: si la fonction f(x) n'est définie que sur un intervalle du type [ b ; a[ ou ] a ; c] et que seule existe une limite à gauche ou à droite de "a" alors la représentation graphique de f(x) dispose toujours d'une asymptote .
Exemple
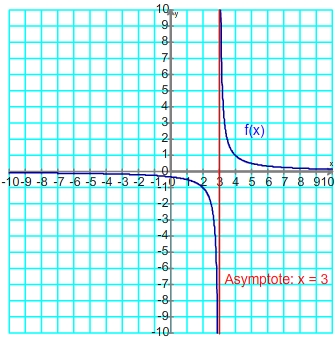
Si f(x) = 1
x-3
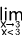 f(x) =
f(x) =  et
et 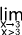 f(x) =
f(x) = 
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
