Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Limite finie ou infinie d'une fonction à l'infini
Limite d'une fonction en "plus" l'infini
Soit "f" une fonction dont l'ensemble de définition s'étend jusqu'à 
(incluant un intervalle de la forme [a ; [ ou ] a ; [ )
Cette fonction "f" tend vers une limite réelle finie "l" en si pour tout intervalle ouvert incluant "l" il existe une valeur de x0 assez grande pour que l'image de l'intervalle [x0 ; [ par "f" soit incluse dans cet intervalle. on note alors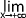 
f(x) = l
Pour pour une démonstration l'intervalle incluant "l" peut être centrée sur cette valeur et donc de forme ] l-b ; l+b [ où b" est un réel positif.
Cette tend fonction "f" tend vers en si pour tout intervalle ] a ; [ il existe une valeur de x0 assez grande pour que l'image de l'intervalle [x0 ; [ par "f" soit incluse dans ] a ; [ . on note alors 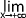f(x) =
Cette tend fonction "f" tend vers 
en si pour tout intervalle ] ; a [ il existe une valeur de x0 assez pour que l'image de l'intervalle [x0 ; [ par "f" soit incluse dans ] ; a [ . on note alors 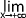f(x) =
Limite de quelques fonction usuelles en "plus
Limite d'une fonction en "moins" l'infini
Soit "f" une fonction dont l'ensemble de définition s'étend jusqu'à (incluant un intervalle de la forme ] ; a [ ou ] ; a ] )
Cette fonction "f" tend vers une limite réelle finie "l" en si pour tout intervalle ouvert incluant "l" il existe une valeur négative de x0 assez grande en valeur absolue pour que l'image de l'intervalle ] ; x0[ par "f" soit incluse dans cet intervalle. on note alors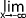 
f(x) = l
Cette tend fonction "f" tend vers en si pour tout intervalle ] a ; [ il existe une valeur négative de x0 assez grande en valeur absolue pour que l'image de l'intervalle ] ; x0[ par "f" soit incluse dans] a ; [ . on note alors 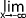f(x) =
Cette tend fonction "f" tend vers en si pour tout intervalle ] ; a [ il existe une valeur négative de x0 assez grande en valeur absolue pour que l'image de l'intervalle ] ; x0[ par "f" soit incluse dans ] ; a [ . on note alors f
(x) =
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
