Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Limite infinie d'une fonction en un point
Limite infinie d'une fonction à gauche d'un point
Soit "f" une fonction dont l'ensemble de définition inclut un intervalle de la forme ] b ; a [
On dit "f" tend vers 
à gauche du réel "a" si quel que soit l'intervalle ] c ; [ il existe une valeur x0 appartenant à l'intervalle ] b ; a [ assez proche de "a" pour que l'image de l'intervalle [x0 ; a [ soit incluse dans ] c ; [. On note alors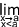 
f(x) =
On dit "f" tend vers 
à gauche du réel "a" si quel que soit l'intervalle ] - ; c [ il existe une valeur x0 appartenant à l'intervalle ] b ; a [ assez proche de "a" pour que l'image de l'intervalle [x0 ; a [ soit incluse dans ] ; c [. On note alors 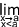f(x) =
Limite infinie d'une fonction à droite d'un point
les définitions précédentes peuvent être adaptées pour définir les limite à droite d'un point.
Soit "f" une fonction dont l'ensemble de définition inclut un intervalle de la forme ] a ; b [
On dit "f" tend vers à droite du réel "a" si quel que soit l'intervalle ] c ; [ il existe une valeur x0 appartenant à l'intervalle ] a ; b [ assez proche de "a" pour que l'image de l'intervalle ] a ; x0 ] soit incluse dans ] c ; [. On note alors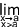 
f(x) =
On dit "f" tend vers à droite du réel "a" si quel que soit l'intervalle ] - ; c [ il existe une valeur x0 appartenant à l'intervalle ] a ; b [ assez proche de "a" pour que l'image de l'intervalle ] a ; x0 ] soit incluse dans ] ; c [. On note alors 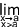f(x) =
Limites identiques à gauche et à droite d'un point
Si la limite à gauche et à droite d'un point "a" sont identiques c'est à dire si 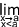f(x) = 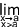f(x) alors on peut se contenter de parler de limite en "a" et noter 
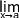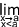f(x) = 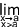f(x) = f(x)
Exemples de limites infinies un point
Si f(x) = 1 alors:
x
- 
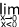f(x) =
- 
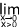f(x) =
Si f(x) = 1 alors:
x2
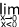- f(x) =
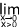- f(x) =
Soit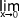 
f(x) =
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
