Analyse - Cours Terminale S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Analyse - Cours Terminale S

Analyse - Cours Terminale S

Limite d'une somme, d'un produit, d'un quotient ou de la composée de deux fonctions

Si une fonction peut être exprimée à partir de deux autres fonctions f(x) et g(x) alors sa limite peut dans de nombreux cas être déduite de celles de f(x) et g(x). Les limites étudiée ici peuvent aussi bien concerné un réel que ou

Somme de deux fonctions

Addition de deux fonctions de limites finies

Si f(x) et g(x) sont deux fonctions de limites respectives l et l' alors leur somme, c'est à dire la suite f(x) + g(x) admet aussi une limite finie:

Addition d'une fonction de limite finie et d'une fonction de limite infinie

Si f(x) est une fonction de limite finie et g(x) une fonction de limite infini alors leur somme tend vers l'infini:

Si lim g(x) =  alors  lim f(x) + g(x) =  et si Si lim g(x) =  alors  lim f(x) + g(x) = 

Addition de deux fonctions de limites  infinies

Si f(x) et g(x) sont deux fonctions de limites infinies identiques ( ou ) alors leur somme possède aussi une limite infinie:

Si lim f(x) =  et  lim g(x) ₌ alors  lim f(x) + g(x) =

Si lim f(x) =  et  lim g(x) ₌  alors  lim f(x) + g(x)  = 

Par contre, si f(x) et g(x) sont deux fonctions de limites infinies différentes (l'une tend vers et l'autre vers ) alors on aboutit à une forme dite "indéterminée", c'est à dire qu'il n'existe pas de règle générale on aussi bien avoir une limite qui correspond à un réel, à ou .

Produit de deux fonctions

Multiplication de deux fonctions de limite finie

Si f(x) et g(x) sont deux fonctions de limites respectives l et l' alors leur produit, c'est à dire la suite f(x).g(x) possède aussi une limite finie:

Multiplication d'une fonction de limite finie par une fonction de limite infinie

Si f(x) est une fonction de limite finie "l" et g(x) une fonction de limite infini alors leur produit tend vers l'infini sauf si la limite "l" est nulle:

Pour l > 0 Si lim g(x) =  alors  lim f(x).g(x) = et si Si lim g(x) =  alors  lim f(x).g(x)  = 

Pour l < 0 Si lim g(x) =  alors  lim f(x).g(x)  =  et si Si lim g(x) =  alors  lim f(x).g(x)  = 

Pour l = 0 on obtient une forme indéterminée

Multiplication de deux fonctions de limites infinies

Si f(x) et g(x) sont deux fonctions de limites infinies identiques ( ou ) alors leur produit tend vers :

Si lim f(x) =  et  lim g(x) =  alors  lim f(x).g(x) =

Si lim f(x) =  et  lim g(x) =  alors  lim f(x).g(x) = 

Cependant si f(x) et g(x) sont deux fonctions de limites infinies différentes (l'une tend vers et l'autre vers ) alors on obtient à nouveau une forme indéterminée.

Quotient de deux fonctions

Division de fonctions de limites finies

Si f(x) et g(x) sont deux fonctions de limites respectives l et l' alors non nulles alors leur quotient, c'est à dire f(x)/g(x) possède aussi une limite réelle finie (à condition que l' ne soit pas nulle) et:

Si la limite l' est nulle et l non nulle alors le quotient tend vers l'infini avec un signe qui dépend du signe de "l" et de la suite vn:

si l' = 0 et non l nul   lim f(x)/g(x) = ou

Si l et l' sont nulles alors on obtient une forme indéterminée.

Divison impliquant une fonction de limite finie et une fonction de limite infinie

Si f(x) est une fonction de limite finie "l" et g(x) une fonction de limite infini ( ou ) alors leur quotient (f(x)/g(x)) tend vers "0"

 Si  lim f(x) = l  et  lim g(x) =  ou alors lim f(x)/g(x) = 0 

Si au contraire g(x) est une fonction de limite finie "l" et f(x) une fonction de limite infini ( ou )alors leur quotient f(x)/g(x)) tend vers l'infini:

Pour l' > 0 Si lim f(x) =  alors  lim f(x)/g(x) = et si Si lim f(x) =  alors  lim f(x)/g(x) = 

Pour l' < 0 Si lim f(x) =  alors  lim f(x)/g(x) =  et si Si lim f(x) =  alors  lim f(x)/g(x) = 

Pour l' = 0  alors  lim f(x)/g(x) = ou

Division impliquant deux fonctions de limite infinie

Si f(x) et g(x) sont deux fonctions de limites infinies (  ou  ) alors leur quotient est une forme indéterminée

Composition de deux fonctions

Définition

Une fonction f(x) est dite composée si elle s'exprime comme la succession de deux fonctions g(x) et h(x): f(x) = g(h(x)).  
En d'autre terme un nombre "x" donne une image y=h(x) par une fonction h qui elle même donne une image g(y) par une fonction g.

Exemple

La fonction f(x) = (2x +1)² peut être considérée commme la composée de la fonction afine h(x) = 2x + 1 par la fonction carré g(x) = x².
En effet g(h(x)) = (h(x))²
                           = (2x +1)²

Théorème

Soit f(x) la composée de la fonction h(x) par g(x) telle que f(x) = g(h(x)) alors si h(x) admet une limite "b" en un point a et que g(x) admet une limite "c" au point "b" alors la limite de la fonction f(x) en x0 est b:

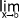si   h(x) = b et g(x) = c alors 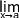f(x) = c

a, b, et c peuvent désigner aussi bien un réel que ou