Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Limites et comparaisons
Limites infinies
Soient f(x) et g(x) deux fonctions définies sur un intervalle de la forme [a ;  [ alors:
[ alors:
Si la fonction g(x) est inférieure à la fonction f(x) sur cet intervalle et que g(x) tend vers  en
en  alors la fonction f(x) tend aussi vers
alors la fonction f(x) tend aussi vers  :
:
 f(x) sur [a ;
f(x) sur [a ;  [et
[et 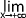 g(x) =
g(x) =  alors
alors 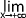 f(x) =
f(x) = 
Si la fonction g(x) est inférieure à la fonction f(x) sur cet intervalle et que f(x) tend vers  en
en  alors la fonction g(x) tend aussi vers
alors la fonction g(x) tend aussi vers  :
:
 f(x) sur [a ;
f(x) sur [a ;  [et
[et 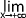 f(x) =
f(x) =  alors
alors 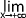 g(x) =
g(x) = 
Ces théorèmes peuvent être adaptés pour les limites en moins l'infini
Soient f(x) et g(x) deux fonctions définies sur un intervalle de la forme ]  ; a ] alors:
; a ] alors:
Si la fonction g(x) est inférieure à la fonction f(x) sur cet intervalle et que g(x) tend vers  en
en  alors la fonction f(x) tend aussi vers
alors la fonction f(x) tend aussi vers  :
:
 f(x) sur]
f(x) sur]  ; a ] et
; a ] et 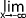 g(x) =
g(x) =  alors
alors 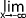 f(x) =
f(x) = 
Si la fonction g(x) est inférieure à la fonction f(x) sur cet intervalle et que f(x) tend vers  en
en  alors la fonction g(x) tend aussi vers
alors la fonction g(x) tend aussi vers  :
:
Si g((x)  f(x) sur ]
f(x) sur ]  ; a ] et
; a ] et 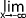 f(x) =
f(x) =  alors
alors 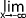 g(x) =
g(x) = 
Limites finies
Conservartion de l'ordre
S'il est possible de comparer deux fonctions sur un intervalle alors leurs limites sur cet intervalle respectent le même ordre.
Soit f(x) et g(x) deux fonction définies sur un intervalle commun [b ; c ] et "a" un point de cet intervalle.
 g(x) sur [b ; c ] alors
g(x) sur [b ; c ] alors 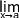 f(x)
f(x) 
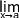 g(x)
g(x)Si f(x)
 g(x) sur [b ; c ] alors
g(x) sur [b ; c ] alors 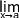 f(x)
f(x) 
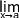 g(x)
g(x)
Le théorème des gendarmes
Soit trois fonctions f(x), g(x) et h(x) définies sur un intervalle de la forme [a ;  [. Si sur cet intervalle la fonction d(x) est comprise entre les fonctions f(x) et h(x) et que ces dernière tendent vers une limite l en
[. Si sur cet intervalle la fonction d(x) est comprise entre les fonctions f(x) et h(x) et que ces dernière tendent vers une limite l en  alors limite de g(x) en
alors limite de g(x) en  est aussi l:
est aussi l:
 [ f(x)
[ f(x)  g(x)
g(x)  h(x) et
h(x) et 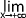 f(x) =
f(x) = 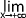 h(x) = l alors
h(x) = l alors 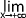 g(x) = l
g(x) = l
De même en moins l'infini:
 ; a ] f(x)
; a ] f(x)  g(x)
g(x)  h(x) et
h(x) et 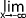 f(x) =
f(x) = 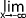 h(x) = l alors
h(x) = l alors 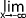 g(x) = l
g(x) = lPour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
