Analyse - Cours Terminale S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Analyse - Cours Terminale S

Analyse - Cours Terminale S

Fonction sinus

Définition

La fonction sinus est la fonction qui à tout réel "x" associe son sinus sin(x). Elle est définie sur l'ensemble des réels (intervalle ]  ; [) et elle est également contiue sur cet intervalle.

Parité

C'est une fonction impaire puisque pour tout "x" sin(-x) = -sin(x), ce qui se traduit pour sa courbe représentative par une symétrie centrale par rapport à l'origine du repère.

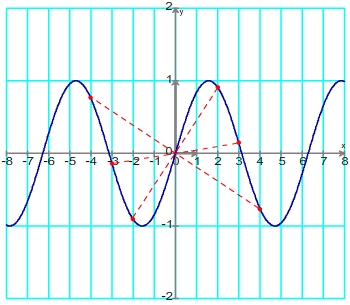
Périodicité

Puisque sin( x + 2π) = sin(x) on qualifie le sinus de fonction périodique de période 2π. Sur une représentation graphique cette périodicité implique que la totalité de la courbe peut être obtenue par translations successives de 2π ou -2π à partir d'une portion de courbe sur un intervalle d'étendue 2π (par exemple [-π ; π] ou [0 ; 2π])

Dérivabilité

par définition

f'(x) =   f(x + h) - f(x)  
                         h

(sin(x))' =   sin(x + h) - sin(x)  
                                 h

(sin(x))' =   sin(x)cos(h) + cos(x)sin(h) - sin(x)  
                                               h

or lim sin(x)cos(h) -sin (x) = sin(x)cos(0) - sin(x)
                                         = sin(x).(cos(0) - 1)
                                         = sin(x).(0)
                                         = 0
donc
(sin(x))' =    cos(x)sin(h)   
                               h
or   sin(h) = 1
              h
donc

(sin(x))' =    cos(x).sin(h)   
                                 h
(sin(x))' =  cos(x).1

(sin(x))' = cos(x)

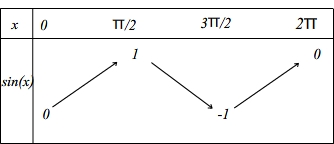
Variations de la fonction sinus

Puisque la fonction sinus présente une périodicité de 2π  il suffit d'étudier ses variations sur l'intervalle [ 0 ; 2π ]

L'étude des ses variations peut être faite à partir de sa dérivée. Puisque sin'(x) = cos(x), la fonction cosinus étant positive sur [0 ; π/2] et [3π/2 ; 2π] et négative sur [ π/2 ; 3π/2] on peut en déduire que la fonction sinus est croissante sur [0 ; π/2] et [3π/2 ; 2π] et décroissante sur [ π/2 ; 3π/2]

On obtient donc le tableau de variation suivant

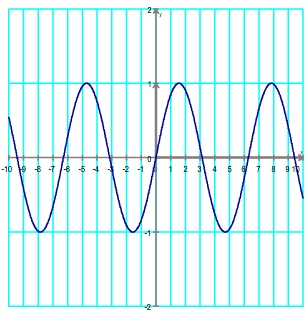
Représentation graphique

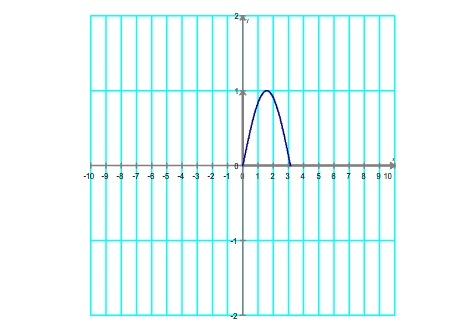
Puisque la fonction sinus est impaire il suffit de tracer sa représentation sur l'intervale [ 0 ; π ]

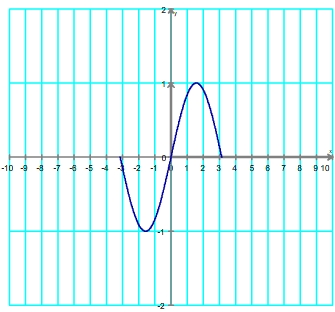
Par symétrie centrale on obtient la représentation sur [-π ; 0] on obtient donc la représentation sur l'intervalle [ -π ; π ] d'étendue 2π

 pour obtenir le reste de la courbe il suffit de répéter cette portiont par translations successives de 2π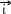 ou -2π