Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Limites et variations
Variations
Soient "a" et "b" deux réels strictement positifs tels que a < b
"a" possède un seul antécédent "a' " par la fonction exponentielle tel que a = exp(a') de même "b" possède un seul antécédent "b'" par la fonction exponentielle tel que b = exp(b').
Puisque fonction exponentielle est strictement croissant on également: a' < b'
De plus:
Ln (a) = ln(exp(a'))
= a'
Ln (b) = ln(exp(b'))
= b'
Donc puisque a' < b on a ln(a) < ln(b)
Pour tous réels strictement positifs "a" et "b", si a<b alors ln(a) < ln(b) ce qui démontre que la fonction logarithme népérien est strictement croissant sur son ensemble de définition.
Dérivation
(exp(lnx))' = (ln'x)exp(ln(x))
x' = (ln x)'.x
1 = (ln'x).x
(ln'(x)) = 1
x
La dérivée de la fonction logaritme néperien est donc la fonction inverse
Cette fonction est bien positive sur l'intervalle ]0;  [ ce qui confirme que la fonction logaritme néperien est bien strictement croissante sur son ensemble de définition
[ ce qui confirme que la fonction logaritme néperien est bien strictement croissante sur son ensemble de définition
Limites
La fonction exponentielle tend vers  en
en  donc la fonction logarithme népérien qui est sa fonction reciproque tend également vers
donc la fonction logarithme népérien qui est sa fonction reciproque tend également vers  en
en 
Par ailleurs la fonction exponentielle tend vers 0 en -inf donc sa fonction réciproque tend vers  en 0
en 0
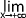 ln(x) =
ln(x) = 
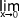 ln(x) =
ln(x) = 
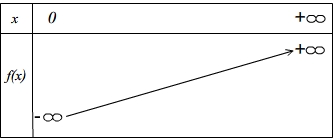
Tableau de variation
Les variations et les limites de la fonction logarithme néperien permettent de dresser son tableau de variation :
Autres limites
Autres limites à connaitre pour la fonction logarithme néperien
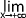 ln(x) = 0
ln(x) = 0x
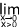 x.ln(x) = 0
x.ln(x) = 0 Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
