Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Intégrale d'une fonction continue de signe quelconque
Définition
La définition d'une intégrale peut être étendue aux fonctions continues dont le signe est quelconque (et pas seulement positif). Aini si "f" est une fonction continue sur un intervalle "I" et que les nombres "a" et "b" appartiennent à cet intervalle alors l'intégrale de la fonction "f" de "a" à "b" est notée 
f(x)dx et cette inégrale correspond à différence entre l'intégrale de "f" en "b" et en "a":
f(x)dx = F(b) - F(a)
Le résultat d'une telle intégrale peut être positif (si la surface supérieure délimitée par la courbe au dessus de l'axe des abscisses est supérieure à celle délimitée par la courbe en dessous de l'axe des abscisses) mais il peut aussi être négatif dans le cas contraire.
Intégrale nulle
Une intégrale est nulle:
- si ses deux bornes sont identiques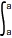 
f(x)dx = 0 en effet 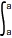f(x)dx = F(a) - F(a) = 0
- si la courbe représentative de la fonction f délimite des surfaces égales de part et d'autre de l'axe des abscisses.(dans ce cas la "partie" positive de l'intégrale compense sa partie "négative"
- si "f" est la fonction nulle.
Inversion des bornes
Deux intégrales d'une même fonction dont les bornes sont inversées ont des valeurs opposées:
f(x)dx = - 
f(x)dx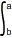En effet f(x)dx = F(b) - F(a) tandis que 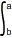f(x)dx = F(a) - F(b) et F(b) - F(a) = - (F(a) - F(b))
Linéarité
L'intégrale du produit d'un réel par une fonction est égale au produt du réel par l'intégrale de cette fonction:
c.f(x)dx = c.f(x)dx
En effet c.f(x)dx = c.F(b) - c.F(a)
= c.( F(b) - F(a) )
= c.f(x)dx
Relation de Chasles
Soient "a", "b" et "c" trois réels quelconques et "f" une fonction inégrale
f(x)dx + 
f(x)dx =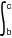 
f(x)dx
En effet:
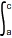f(x)dx = F(b) - F(a) et 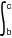f(x)dx = F(c) - F(b)
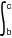Donc f(x)dx + f(x)dx = F(b) - F(a) + F(c) - F(b)
= F(c) - F(a)
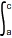= f(x)dx
Positivité
Si une fonction "f" est continue et positive sur un intervalle [a ; b] alors f(x)dx > 0
Comparaison
Si "f" et "g" sont deux fonction continues sur un intervalle [a ; b] telles que pour tout "x" de cet intervalle f(x) 
g(x) alors: f(x)dx g(x)dx
Moyenne
Si une fonction "f" est continue sur un intervalle [ a ; b ] alors la moyenne "m" de cette fonction sur cet intervalle est définie par:
f(x)dx(b - a)
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
