Géométrie - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie - Cours Terminale S
Géométrie - Cours Terminale S
Forme trigonométrique
Module d'un nombre complexe
Le module d'un nombre complexe z = a + ib est noté |z| (comme une valeur absolue) ou "r" et il est défini par la relation |z| = 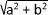
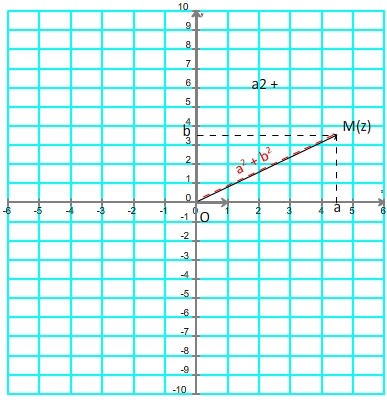
Si le nombre complexe "z" est utilisé comme affixe du point M et du vecteur  (a ; b) alors le module de z correspond aussi à la norme du vecteur
(a ; b) alors le module de z correspond aussi à la norme du vecteur  .
.
Un nombre complexe a même module que son conjugué, que son opposé ainsi que l'opposé de son conjugué:
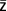 | |-z| = |-
| |-z| = |-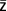 |
|
Dans certains cas il est possible d'exprimer le module d'un nombre complexe, en particulier, si "z" et "z'" sont deux nombres complexes et "n" un entier alors:
Le module d'un produit de deux nombres complexes correspond au produit du module de chacun de ces nombres
 =
= 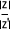
Le module du rapport de deux nombres complexes correspond aux rapport des modules de ces nombres
Le module d'une puissance "n" d'un nombre complexe correspond à la puissance "n" de son module
Cependant attention |z + z'| 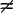 |z| + |z'|, le module de la somme de deux nombres complexe n'est pas équivalent à la somme des modules de chacun de ces nombre. On peut seulement écrire une inégalité dite triangulaire:
|z| + |z'|, le module de la somme de deux nombres complexe n'est pas équivalent à la somme des modules de chacun de ces nombre. On peut seulement écrire une inégalité dite triangulaire:
 |z| + |z'|
|z| + |z'|
Argument d'un nombre complexe
L'argument d'un nombre complexe est noté arg(z) ou θ (lettre grecque thêta), il s'exprime en radian et correspond à l'angle entre le vecteur  d'affixe "z" et l'axe des abscisses
d'affixe "z" et l'axe des abscisses
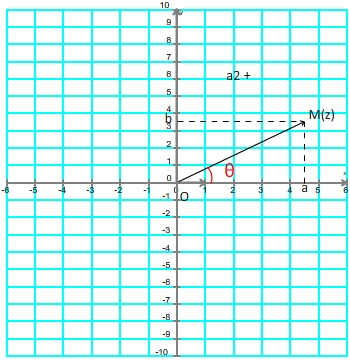
Par conséquent:
- Tous les nombres réels situés sur l'axe des abscisses ont un argument nul (θ = 0 (2π))
- Tous les imaginaires purs situés sur l'axe des ordonnées ont un argument de pi sur 2 (θ = π/2 (2π))
- Le conjugué d'un nombre complexe qui lui est symétrique par rapport l'axe des abscisse possède un argument opposé: arg(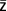 ) = - arg(z) (2π)
) = - arg(z) (2π)
La projection du vecteur  sur l'axe des abscisse correspond à "a" tandis que la projection de
sur l'axe des abscisse correspond à "a" tandis que la projection de  sur l'axe des ordonnées correspond à "b" (voir figure précédente) donc:
sur l'axe des ordonnées correspond à "b" (voir figure précédente) donc:
| |.cos (θ) = a et |
|.cos (θ) = a et | |.sin (θ) = b soit
|.sin (θ) = b soit 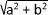 .cos (θ) = a et
.cos (θ) = a et 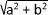 .sin (θ) = b donc:
.sin (θ) = b donc:
cos (θ) = a
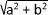
sin (θ) = b
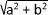
On peut donc déduire cos (θ), sin (θ) et donc θ à partir de la forme algébrique d'un nombre complexe
Notation trigonométrique d'un nombre complexe
Tout nombre complexe z = a + ib peut sécrire sous une forme trigonométrique:
On peut vérifier que cette notation trigonométrique est équivalente à la totation algébrique:
z = r ( cos(θ) + isin(θ) )
= 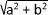 . ( a + ib )
. ( a + ib )
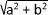
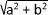
= a.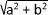 + ib.
+ ib.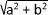
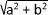
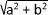
= a + ib
Il est possible de passer de la notation algébrique à la notation trigonométrique grâce aux relations suivantes:
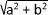
cos (θ) = a
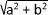
sin (θ) = b
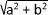
Inversement, on peut aussi passer d'une notation trigonométrique à une notation algébrique à partir de ces relations:
b = r.sin (θ)
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
