Géométrie - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie - Cours Terminale S
Géométrie - Cours Terminale S
Vecteurs coplanaires
Définition
Des vecteurs (au moins au nombre de 3) sont dits coplanaires si leurs représentants appartiennent au même plan.
Par exemple, trois vecteurs  ,
,  et
et  sont dit coplanaires si les vecteurs
sont dit coplanaires si les vecteurs 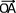 ,
,  et
et 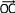 tels que
tels que 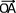 =
=  ,
,  =
=  et
et 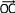 =
=  appartienent au même plan ce qui implique le point correspondant à leur origine (O) ainsi que les points correspondant à leurs extêmités ( A, B et C) font partie d'un même plan.
appartienent au même plan ce qui implique le point correspondant à leur origine (O) ainsi que les points correspondant à leurs extêmités ( A, B et C) font partie d'un même plan.
Conditions de coplanarité
Trois vecteurs  ,
,  et
et  sont coplanaires si et seulement si il on peut exprimer l'un vecteur comme une combinaison des autre, c'est à dire s'il existe deux réels "a" et "b" tels :
sont coplanaires si et seulement si il on peut exprimer l'un vecteur comme une combinaison des autre, c'est à dire s'il existe deux réels "a" et "b" tels :
 = a.
= a. + b.
+ b.
Cette égalité peut également s'écrire
a. + b.
+ b. -
-  = 0
= 0
Si l'on multiplie chaque membre par un réel "c" quelconque on obtient:
c.a. + c.b.
+ c.b. - c.
- c. = 0
= 0
En posant a' = c.a ; b' = c.b et c' = -c cette relation devient:
a'. +b'.
+b'. + c'.
+ c'. = 0
= 0
On peut donc également formuler la condition coplanarité de la manière suivante:
Trois vecteurs  ,
,  et
et  sont coplanaires si et seulement s'il existe trois réels " a' " et " b' " et " c' " tels :
sont coplanaires si et seulement s'il existe trois réels " a' " et " b' " et " c' " tels :
 +b'.
+b'. + c'.
+ c'. = 0
= 0
Remarque: si deux des trois vecteurs sont colinéaires alors les trois vecteurs sont nécessairement coplanaires.
Caractérisation d'un plan à partir de la condition de coplanarité
Soit P un plan auquel appartient un point "O", deux vecteurs  et
et  non colinéaires et deux vecteurs
non colinéaires et deux vecteurs 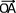 et
et  tels que
tels que 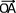 =
=  ,
,  =
=  . L'ensemble des points"M" appartenant au plan P sont tels que les vecteurs
. L'ensemble des points"M" appartenant au plan P sont tels que les vecteurs 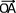 ,
,  et
et  soient colinéaires.
soient colinéaires.
Par conséquent le plan P est l'ensemble des points M définis par la relation:
 = a.
= a.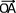 + b.
+ b. où "a" et "b" sont des réels
où "a" et "b" sont des réels
D'une manière général un plan peut être caractérisé par un point et deux vecteurs colinéaires.
Conséquences:
- Si deux plans P et P' sont caractérisés par le même point et les mêmes vecteurs alors ces deux plans sont confondus.
- Si deux plans P et P' sont caractérisés les même vecteurs mais par des points différents alors les plans P et P' sont parallèles.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
