Géométrie - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie - Cours Terminale S
Géométrie - Cours Terminale S
Produit scalaires de deux vecteurs dans l'espace
Définition
Soient 
et 
sont deux vecteurs quelconques de l'espace, A, B et C trois points tels que 
= et 
= . Quels que soient les points A, B et C il existe au moins un plan P contenant les vecteurs et (Si les vecteurs sont colinéaires il y en a une infinité sinon il n'y en qu'un). Le produit scalaire . = . dans l'espace se ramène donc au prdduit scalaire dans le plan P.
Calculer un produit scalaire
Puisque qu'on peut toujours ramener un produit scalaire dans l'espcace à un produit scalaire dans un plan, son expression reste la même:
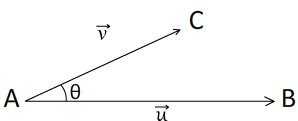
. = AB.AC.cos(θ) = ||||.||||.cos(θ)
Le point " C' " est la projection orthogonale de "C" sur AB c'est à dire le point appartenant à AB tel que MM' soit perpendiculaire à AB
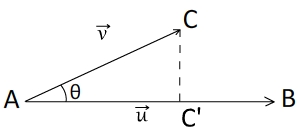
L'expression du produit scalaire peut s'écrire:
. = AB.AC'
Car AC'=AC.cos(θ)
D'après ces expressions, le produit scalaire de deux vecteurs n'est nul qu'à l'une de ces conditions:
- Au moins l'un des vecteurs est nul
- L'angle θ est de π (2π), les deux vecteurs sont donc orthogonaux.
2
Expression analytique
Si les vecteurs et ont pour coordonnées (x ; y ; z) (x' ; y'; z') alors leur produit scalaire peut être exprimé à partir ces coordonnées:
. = x.x' + y.y' + z.z'
Propriétés du produit scalaire dans l'espace
Le propriétés sont les mêmes que dans un plan.
La commutativité du produit scalaire :
et , . = .
Commutativité des facteurs réels :
et et toute constante réelle k: k( . ) = (k) . = . (k)
Distributivité:
, et 
: .( + ) = . + .
Identités remarquables:
et : ( + )2 = 2 + 2.+ 2
et : ( - )2 = 2 -2.+ 2
et : ( + ).( - ) = 2 - 2
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
