Statistiques et probabilités - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques et probabilités - Cours Terminale S
Statistiques et probabilités - Cours Terminale S
Indépendance de deux événements
Définition
On dit que deux événements A et B sont indépendants si la réalisation de l'un n'a aucune influence sur la réalisation de l'autre. Par conséquent:
La probabilité de B sachant que A est réalisé ne dépend pas de A donc PA(B) = P(B)
La probabilité de A sachant que B est réalisé ne dépend pas de B donc PB(A) = P(A)
Exemple: L'évenement lancer un dé est indépendant de l'évenement choisir une boule noire ou blanche dans un sac
Probabilité d'une intersection d'événements
Si A et B sont deux événements de probabilités non nulles alors
P(A  B) = PA(B).P(A) = PB(A).P(B)
B) = PA(B).P(A) = PB(A).P(B)
Si les événements A et B sont indépendants alors PA(B) = P(B) et PB(A) = P(A) donc:
P(A  B) = P(B).P(A) = P(A).P(B)
B) = P(B).P(A) = P(A).P(B)
Si A et B sont deux événements indépendants alors P(A  B) = P(A).P(B)
B) = P(A).P(B)
Démontrer que deux événements sont indépendants
Pour prouver que deux événements A et B sont indépendants, on peut utiliser un arbre pondéré pour démontrer au choix:
- que PA(B) = P(B)
- que PB(A) = P(A)
- que P(A  B) = P(A).P(B)
B) = P(A).P(B)
Evénements contraires
Soient A et B deux événements indépendants de probabilités non nulles, 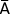 et
et 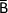 sont leurs événements contraires respectifs.
sont leurs événements contraires respectifs.
Comme pour tout événement et son événement contraire on a:
PA(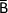 ) = 1 - PA(B)
) = 1 - PA(B)
Puisque A et B sont indépendants on a PA(B) = P(B) donc la relation précédente devient:
PA(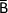 ) = 1 - P(B)
) = 1 - P(B)
PA(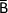 ) = P(
) = P(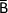 )
)
Ce qui démontre que A et 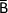 sont indépendants, en suivant une démarche analogue on peut également montrer que
sont indépendants, en suivant une démarche analogue on peut également montrer que 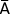 et B sont indépendants, tout comme
et B sont indépendants, tout comme 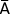 et
et 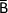 .
.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
