Statistiques et probabilités - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques et probabilités - Cours Terminale S
Statistiques et probabilités - Cours Terminale S
Fluctuation et estimation
Fluctuation et prise de décision
Si Xn est une variable aléatoire qui suit une loi binomiale de paramètres "n" et "p" alors on peut définir à partir de cette dernière une autre variable notée Fn telle que Fn = Xn, cette dernière correspond à la fréquence de succès.
n
Pour tout réel α appartenant à l'intervalle ]0 ; 1[ il existe un réel uα tel que:
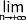P(Fn 
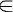In) = 1 - α avec In l'intervalle [ p - uα. 
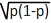; p + uα. ]
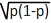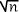
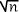
L'intervalle In correspond à un intervalle de fluctuation asymptotique de Fn au seuil de 1 - α
En particulier, lorsque α = 0,05 alors uα = 1,96 et 1 - uα= 0,95: In correspond à l'intervalle de fluctuation au seuil de 95 %.
Attention cet intervalle n'est valide que si n 
30, n.p 5 et n.(1-p) 5
On peut utiliser ce seuil pour une prise de décision, par exemple si l'on étudie un caractère sur échantillon de population composé de "n" éléments, la proportion de ce caractère étant "p" pour la population totale alors on peut valider l'hypothèse que la proportion est aussi de "p" sur l'échantillon à condition que la fréquence de ce caractère sur l'échantillon appartienne à l'intervalle In correspondand à l'intervalle de fluctuation au seuil de 95 %, sinon l'hypothèse est rejetée.
Estimation
Soit une variable aléatoire Xn suivant une loi binomiale de paramètres "n" et "p", alors pour tout réel p tel que 0 < p < 1 , il existe un entier "n" au-delà duquel P ( p - 1 
Fn p + 1 ) > 0,95
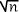
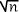
Fn est une variable aléatoire qui associe à tout échantillon de taille "n" d'une population, la proportion "p" d'un caractère étudié.
Si "n" est assez grand alors la probabilité que l'intervalle [ Fn - 1 ; Fn + 1 ] contienne la proportion "p" est
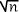
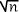
supérieure à 0,95.
[ Fn - 1 ; Fn + 1 ] est un intervalle de confiance de niveau de confiance de 95% pour la fréquence "f" d'un
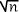
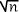
caractère sur un échantillon de taille "n" extrait d'une population où la proportion de ce caractère est "p"
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
