Statistiques et probabilités - Cours Terminale S

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Statistiques et probabilités - Cours Terminale S

Statistiques et probabilités - Cours Terminale S

Loi à densité sur un intervalle

Définition d'une fonction de densité de probabilité

Une fonction "f" définie sur un intervalle "I" de l'ensemble des réels est une fonction de densité de probabilité si les trois conditions suivantes sont vérifiées:

1) La fonction "f" est continue sur l'intervalle "I"

2) Elle reste positive sur la totatlité de l'intervalle "I"

3) L'intégrale de la fonction "f" de la borne inférieures de "I" à sa borne supérieure est égale à 1

Remarques

La condition 3) est équivaut à dire que la courbe représentative de la fonction "f" délimite par rapport à l'axe des abscisses un domaine dont l'aire est de "1".

Si "I" est un intervalle, dont les bornes sont finies, de forme [ a ; b ] alors la condition n°3 peut être traduite par l'égalité f(x)dx = 1

L'intervalle "I" n'est pas obligatoire munies de bornes finie, sa borne inférieure peut être  et sa borne supérieure peut être 

Exemples de fonctions de densité de probabilité

"f" est la fonction définie par la relation f(x) = x² sur l'intervalle [0 ; 1]    
                                                                           3
"f" est continue [0 ; 1]
"f" est positive [0 ; 1]
L'une de ses primitive est F(x) = x³ donc 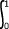f(x)dx = 1³ -  0³ = 1    
"f" est donc bien une fonction à densité de probabilité 

"g" est la fonction définie par la relation g(x) =  x  sur l'intervalle [0 ; 2]  
                                                                             2
"g" est continue [0 ; 2]
"g" est positive [0 ; 2]
L'une de ses primitive est F(x) = x² donc 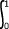g(x)dx = 2² -  0² = 1
                                                    4                            4      4
"g" est donc bien une fonction à densité de probabilité 

Variable aléatoire à densité sur un intervalle

Une variable aléatoire X suit une loi de densité "f" sur un intervalle "I" si pour tout intervalle [a;b] inclus dans "I", la probabilité de l'événement X 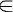[a;b] (que l'on peut noter P( a X b) est égale à l'aire du domaine délimité entre la courbe "f" et l'axe des abscisses du point "a" au point "b" ce qui correspond à la valeur de l'intégrale f(x)dx

Propriétés

- En raison de la définition de la fonction de densité de probabilité, si "a" et "b" correspondent aux bornes de l'intervalle "I" alors f(x)dx = 1.
- Si [a;b] et [c;d] sont des intervalles inclus dans "I" alors P(X 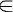[a;b] U [c;d]) = P (X [a;b]) + P(X [c;d])

- Si "a" est un réel appartenant à "I" alors P(X=a) = 0, la probabilité ne peut être non nulle que sur un intervalle.

- Une conséquence de la propriété précédente est l'égalité entre les probabilités suivantes, pour tout a et b de l'intrevalle "I" P( a X b) = P( a < X b) = P( a X < b) = P( a < X < b)

- Pour tout réel "a" de I,  P( X>a) = 1 - P(X<a)

Espérance d'une variable aléatoire à densité sur un intervalle

L'espérance E(X) d'une variable aléatoire suivant la fonction de densité "f" sur un intervalle [a ; b] est définie par la relation: