Statistiques et probabilités - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques et probabilités - Cours Terminale S
Statistiques et probabilités - Cours Terminale S
Lois normales
Théorème de Moivre-Laplace
Si Xn est une variable aléatoire qui suit une loi biomiale de paramètres n et p avec 0 < n < 1 alors on peut définir une nouvelle variable aléatoire Zn par la relation suivante:
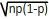
Cette nouvelle variable est dite aléatoire et centrée, elle possède une espérance nulle et il est possible d'exprimer les probabilités qui lui sont associées:
Si "a" et "b" sont deux réels quelconques tels que a < b alors:
 Zn
Zn  b ) =
b ) =  1 . exp(-0,5.x2)
1 . exp(-0,5.x2)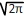
Loi normale centrée réduite N(0;1)
La loie normale centrée réduite que l'on note N(0 ; 1) est la loi suivie par une variable aléatoire dont la fonction de densité est définie sur la totalité de l'ensemble des réels par:
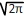
Si une variable aléatoire X suit cette loi alors pour tous réels "a" et "b" tels que a < b :
 X
X  b ) =
b ) =  1 . exp(-0,5.x2)
1 . exp(-0,5.x2)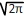
Propriétés de la loi normale centrée réduite N(0;1)
La fonction "f" associée à cette loi est paire donc sa courbe représentative est symétrique par rapport l'axe des ordonnées par conséquent, pour tout réel "a" positif:
 a) = P( X
a) = P( X  a)
a) P( X
 0) = P( X
0) = P( X  0) = 0,5
0) = 0,5P(0
 X
X  a) = P (-a
a) = P (-a  X
X  0)
0)P(-a
 X
X  a) = 1 - 2P( X
a) = 1 - 2P( X  a) = 1 - 2P( X
a) = 1 - 2P( X  -a)
-a)
Si X est une variable aléatoire qui suit la loi normale centrée réduite pour tout réel α tel que 0 < α < 1 alors il existe un seul et unique réel noté uα tel que: P( uα  X
X  uα ) = 1 - α
uα ) = 1 - α
Si X est une variable aléatoire suivant une loi normale centrée alors:
Sa variance est 1: V(X) = 1
Son écart-type est 1: σ(X)= 1
Loi normale ( μ , σ2)
Une variable aléatoire X suit une loi normale ( μ , σ2) à condition qu'une variable aléatoire Z définie par la relation Z = X - μ suivent une loi normale centrée réduite.
σ
Sa variance est σ2: V(X) = σ2
Son écart-type est σ: σ(X)= σ
Valeurs approchées de quelques probabilités:
P( μ - σ  X
X  μ + σ)
μ + σ)  0,68
0,68
P( μ - 2σ  X
X  μ + 2σ)
μ + 2σ)  0,95
0,95
P( μ - 3σ  X
X  μ + 3σ)
μ + 3σ)  0,997
0,997
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
