Statistiques et probabilités - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques et probabilités - Cours Terminale S
Statistiques et probabilités - Cours Terminale S
Loi uniforme sur un intrevalle de type [a ; b]
Fonction définissant une loi uniforme
Une fonction de densité de probabilité "f" suit une loi uniforme sur un intervalle [a ; b] si "f" est une fonction constante f(x) = 1
b - a
"f" est bien continue
f est positive (puisque b > a)
L'une de ses primitive est F(x) = x donc:
b - a
f(x)dx = b - a
b - a b - a
= b -a
b -a
= 1
Les trois conditions pour que "f" soit une fonction de densité de probabilité sur [a ; b ] sont bien vérifiées
Variable aléatoire suivant un loi uniforme
Si X est une variable aléatoire suivant une loi uniforme sur un intervalle [a ; b] dont la densité de probabilité est la fonction "f" alors pour tous réels "c" et "d" appartenant à [a ; b], alors:
P( c 
X d) =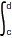 
f(x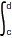)dx
= 1 dx
b - a
= d - c
b - a b - a
= d - c
b - a
X d) = d - c b - a
Espérance d'une variable aléatoire suivant un loi uniforme
Soit X une variable aléatoire suivant une loi uniforme sur [a ; b], par définition son espérance est donnée par la relation suivante:
E(X) = x.f(x)dx
E(X) = x. 1 dx
b-a
La primitive de "x" est 0,5.x2 donc l'espéreance a pour valeur:
E(X) = 0,5 . b2 - 0,5 . a2
b-a b-a
E(X) = 0,5 (b2 - a2)
b-a
E(X) = 0,5 (b - a).(b + a)
b-a
E(X) = 0,5.(b +a)
E(X) = 0,5.(b +a)
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
