Statistiques et probabilités - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Statistiques et probabilités - Cours Terminale S
Statistiques et probabilités - Cours Terminale S
Lois exponentielles
Définition
On dit qu'une variable aléatoire X suit une loi exponentielle de paramètre λ si la fonction de densité de probabilité "f" définie sur l'intervalle [ 0 ; 
[ est de la forme:
On peut vérifier que "f" possède les caractèristiques d'une fonction de densité de probabilité:
- Elle est bien continue
- Elle possitive sur son ensemble de définition (une exponentielle est toujours positive)
- Puisque la primitive de "f" est - e-λx :
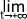
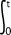λ.e-λxdx = 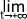-e-λt - -e-λ.0
= 0 - -1
= 1
Conclusion la fonction "f" définie par f(x) = λ.e-λx est bien une fonction de densité sur [ 0 ; [
Expression des probabilités
Si "a" et "b" sont deux réels positifs tels que a < b alors:
P ( a 
X b ) = 
f(x)dx
= λ.e-λxdx
= -e-λ..b - (-e-λ..a)
= e-λ..a- e-λ..b
X b ) = e-λ..a- e-λ..b P ( X a ) =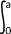 
f(x)dx
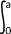= λ.e-λxdx
= -e-λ..a - (-e-λ.0 )
= -e-λ..a + 1
= 1 - e-λ..a
a ) = = 1 - e-λ..a
a < X est l'évenement contraire de X a dont P ( a < X ) = 1 - P ( X a )
= 1 - ( 1 - e-λ..a)
= e-λ..a
Espérance
Par définition l'espérance d'une variable aléatoire X qui suit une loi de densité exponentielle est :
E(X) = 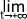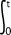x.λ.e-λxdx
L'une des primitives de x.λ.e-λx est -(x + 1 ).e-λx
λ
En effet:( -(x + 1 ).e-λx )' = [ -(x + 1 )]'.e-λx + -(x + 1 )(.e-λx)'
λ λ λ
= (-1).e-λx + - (x + 1 )(-λe-λx)
λ
= -e-λx + ( λx +1)e-λx
= -e-λx + λxe-λx + e-λx
= λxe-λx
Ce qui permet d'obtenir:
E(X) = 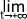-(t + 1 ).e-λt - -(0 + 1 )e-λ..0
λ λ
E(X) = 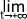-t.e-λt - 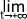e-λt + (0 + 1 ).1
λ λ
E(X) = 0 - 0 + 1
λ
E(X) = 1
λ
Si X est une variable aléatoire qui suit une loi de densité exponentielle de paramètre λ alors E(X) = 1
λ
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
