Géométrie
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie
Géométrie
Coordonnées d'un vecteur
Définition
Les coordonnées d'un vecteur  correspondent aux coordonnées Du point M tel que
correspondent aux coordonnées Du point M tel que  =
= 
Si le point M a pour coordonnées M(x;y) alors les cordonnées du vecteur  sont
sont  (x;y)
(x;y)
Remarque: les coordonnées d'un vecteur sont parfois notée 
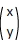 avec l'ordonnée en haut et l'abscisse en bas.
avec l'ordonnée en haut et l'abscisse en bas.
Exemple:
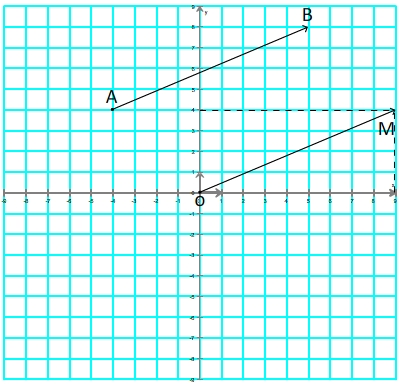
Le vecteur
 est égal au vecteur
est égal au vecteur  (ils ont même direction, même sens et même longeur)
(ils ont même direction, même sens et même longeur)Puisque le point M a comme coordonnées (9;4) le vecteur
 à les coordonnées:
à les coordonnées:  (9;4)
(9;4)
Calculer les coordonnées d'un vecteur à partir de celles de ses extrémités
Soit un vecteur  défini par les points A(xA;yA) et B(xB;yB) alors:
défini par les points A(xA;yA) et B(xB;yB) alors:
- l'abscisse du vecteur correpond à la différence des abscisses des points A et B
- l'ordonnée du vecteur correspond à la différence des ordonnées des points A et B
 ( xB – xA ; yB – yA)
( xB – xA ; yB – yA)
Exemple
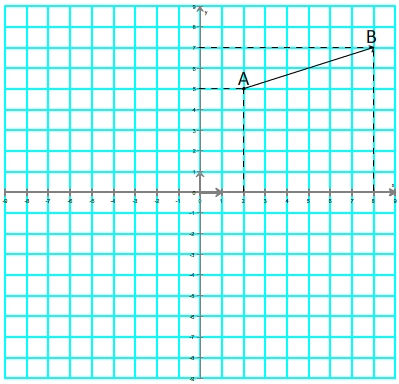
 (8 -2 ; 7 - 5 ) soit
(8 -2 ; 7 - 5 ) soit  ( 6 ; 2 )
( 6 ; 2 )
Vecteur identiques
Si deux vecteurs sont identiques alors leur coordonnées sont les mêmes
Si les points A(xA;yA), B(xB;yB), C(xC;yC) et D(xD;yD) permettent de définir les vecteur  (xB – xA : yB – yA) et
(xB – xA : yB – yA) et 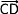 (xD – xC; yD – yC) alors:
(xD – xC; yD – yC) alors:
xB – xA = xD – xC et yB – yA = yD – yC
Exemple
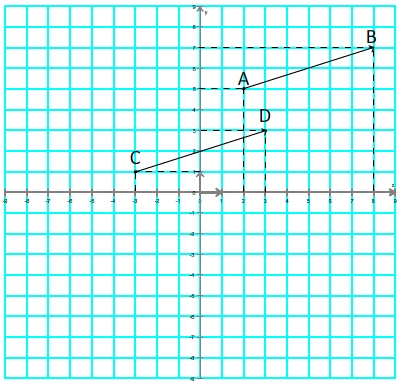
Le vecteur
 a pour coordonnées (8-2; 7-5) soit
a pour coordonnées (8-2; 7-5) soit  (6;2)
(6;2)Le vecteur
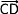 a pour coordonnées (3-(-3); 3-1) soit
a pour coordonnées (3-(-3); 3-1) soit 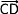 (6;2)
(6;2)Puisque leur coordonnées sont les mêmes ces deux vecteurs sont identiques:
 =
= 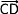
Vecteurs opposés
Si deux vecteurs sont opposés alors leurs abscisses ainsi que leur ordonnées sont opposées
Si  (xu; yu) et
(xu; yu) et  (xv; yvv) sont opposés (
(xv; yvv) sont opposés ( = -
= - ) alors:
) alors:
xu = -xv
yu = -yv
Exemple
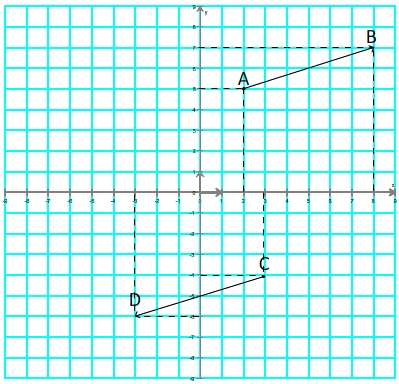
Le vecteur
 a pour coordonnées (8-2; 7-5) soit
a pour coordonnées (8-2; 7-5) soit  (6;2)
(6;2)Le vecteur
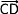 a pour coordonnées (-3-3); -6-(-4)) soit
a pour coordonnées (-3-3); -6-(-4)) soit 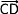 (-6;-2)
(-6;-2)Le vecteur
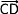 est donc l'opposé du vecteur
est donc l'opposé du vecteur  :
:  = -
= - 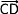
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
