Géométrie
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie
Géométrie
Multiplication d'un vecteur par un réel
Propriétés d'un vecteur obtenu par multiplication
Tout vecteur peut  être multuplié par un réel "a", le vecteur a.
être multuplié par un réel "a", le vecteur a. possède alors:
possède alors:
- la même direction que le vecteur 
- le même sens que le vecteur  si "a" est positif et un sens opposé à celui de
si "a" est positif et un sens opposé à celui de  si "a" est négatif
si "a" est négatif
- une longueur correspondant à "a" fois celle de 
Si "a" est nul alors le produit correspond au vecteur nul 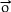
Si  est le vecteur nul alors le produit correspond aussi au vecteur nul
est le vecteur nul alors le produit correspond aussi au vecteur nul 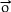
Exemple
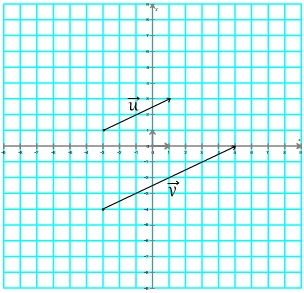
Le vecteur
 correspond à deux fois le vecteur
correspond à deux fois le vecteur  :
:  = 2.
= 2.
Coordonnées d'un vecteur obtenu par multiplication
Si  est un vecteur de coordonnées
est un vecteur de coordonnées  (x;y) alors le produit a.
(x;y) alors le produit a. est un vecteur dont l'abscisse est a.x et l'ordonnée a.y
est un vecteur dont l'abscisse est a.x et l'ordonnée a.y
 (a.x; a.y)
(a.x; a.y)
Exemple
si le vecteur  a pour coordonnée (-2 ; 4) alors le vecteur
a pour coordonnée (-2 ; 4) alors le vecteur  = 3.
= 3. a pour coordonnées
a pour coordonnées  (3.(-2); 3.4) soit
(3.(-2); 3.4) soit  (-6;12)
(-6;12)
Réciproquement, si un vecteur  a pour coordonnées
a pour coordonnées  (b.x ; b.y) et un vecteur
(b.x ; b.y) et un vecteur  apour coordonnées
apour coordonnées  (x;y) alors le vecteur peut être exprimé sous forme du produit
(x;y) alors le vecteur peut être exprimé sous forme du produit  = b.
= b.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
