Géométrie
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie
Géométrie
Relation de Chasles
Enoncé et application de la relation Chasles
La relation de chasle est un cas particulier d'addition de vecteurs, elle ne peut s'appliquer que lorsque l'extrémité du premier vecteur correspond au même point que l'origine du deuxième vecteur, dans ce cas le vecteur somme possède la même origine que le premier vecteur et a la même extrémité que le second vecteur.
Exemples:
 +
+  =
= 
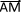 +
+ 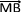 =
= 
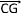 +
+  =
= 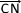
Remarque: le vecteur somme possède des coordonnées qui ne dépendent pas du point commun au deux vecteurs ajouté.
Simplifier une expression vectorielle avec la relation de Chasles
Lorsqu'une expression consiste en une somme de plusieurs vecteurs il est parfois possible d'utiliser la relation de Chasles pour la simplifier.
Exemple d'expression simplifiable:  +
+  +
+  +
+ 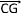
La première étape consiste à rassembler les vecteurs qui possèdent des point communs
Exemple:  +
+  +
+  +
+ 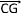 =
=  +
+  +
+ 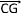 +
+ 
La deuxième étape consiste à vérifier si certains points sont communs à l'origine d'un vecteur et à l'origine de l'autre afin de pouvoir appliquer la relation de Chasles.
Exemple:
- C'est le cas de  et
et  donc :
donc :  +
+  =
= 
- C'est le cas de 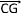 +
+  donc :
donc : 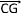 +
+  =
= 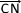
L'expression devient donc  +
+  +
+  +
+ 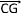 =
=  +
+ 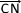
La troisième étape consiste à vérifier si une simplification supplémentaire est possible.
Exemple: dans  +
+ 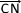 le point C est l'extrémité du premier vecteur mais aussi l'origine du deuxième, on peut de nouveau utiliser la relation de Chasle.
le point C est l'extrémité du premier vecteur mais aussi l'origine du deuxième, on peut de nouveau utiliser la relation de Chasle.
 +
+ 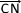 =
= 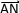
Dans cet exemple la relation de Chasle permet donc de passer de la somme  +
+  +
+  +
+ 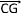 au vecteur unique
au vecteur unique 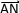
Décomposition d'un vecteur en une somme de vecteurs
La relation de Chasle peut également être utilisée pour obtenir une somme de vecteurs à partir d'un seul et unique vecteur, en effet si  +
+  =
=  alors on a aussi
alors on a aussi  =
=  +
+  .
.
D'une manière générale pour un vecteur  et tout point M quelconque:
et tout point M quelconque:  =
= 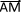 +
+ 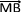
En général le point M intermédiaire utilisé pour décomposé un vecteur n'est pas choisi au hasard, on utilise souvent un point particulier qui permet de répondre à un problème, effectuer une comparaison, etc.
Si par exemple on choisit M comme le milieu du segment [AB] alors ont a 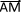 =
= 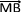 ce qui conduit à
ce qui conduit à  = 2
= 2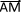 ou
ou  = 2
= 2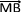
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
