Géométrie

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Géométrie

Géométrie

Vecteurs et translations

La translation

Une translation est définie à partir de deux points A et B du plan: elle transforme le point A en point B mais elle transforme aussi, de la même manière, tout point M du plan en un point M'

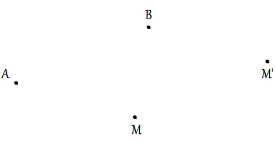
Si un point M' est l'image du point M par la translation qui transforme A en B alors les segments [AM'] et [MB] ont même milieu et reciproquement si des segments [AM'] et [MB] ont le même milieu alors on peut dire que M' est l'image de M par la translation qui transforme A en B

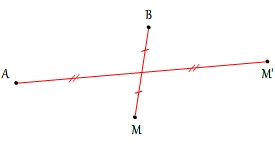
Si [AM'] et [MB] ont le même milieu on peut aussi dire
- que B est l'image de A par la translation qui transforme M en M'
- que M est l'image de M' par par la translation qui transforme B en A
- que A est l'image de B par la translation qui transforme M' en M
- que M' est l'image de B par la translation qui transforme A en M
etc

Parallélogramme et translation

Si une translation transforme A en B et M en M' alors le quadrilatère ABM'M est un parallélogramme

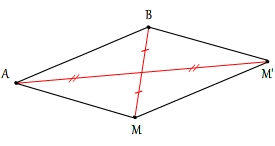
En effet, d'après ce qui précède les segments [AM'] et [MB] on même milieu ce qui constitue une propriété caractéristique des parallélogrammes.

La réciproque est égamlement vraie: si le quadrilatère ABM'M est un parallélogramme alors la translation qui transforme A en B transforme aussi M en M'.

Vecteur associé à une translation

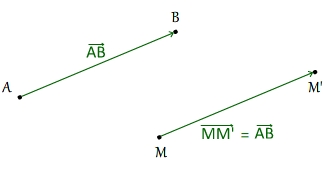
On associe le vecteur  à la translation qui transforme A en B

Si M'est l'image de M par la translation de vecteur  alors  =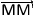 

Vecteurs égaux

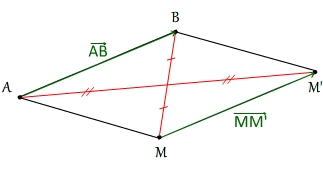
Les vecteurs  et  sont égaux:
- si et seulement si Les segments [AB] et [MM'] ont la même longueur, sont orientés dans le même sens, les droite (AB) et (MM') sont parallèles.
- si et seulement si le quadrilatère ABM'M est un parallélogramme.
- si et seulement si les segments [AM'] et [MB] ont le même milieu.

 
Si plusieurs vecteurs sont égaux ( =  =  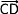etc) alors on utiliser un représentant de ces vecteurs que l'on note, en général avec une seul lettre (par soucis de simplification ) comme par exemple