Géométrie
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Géométrie
Géométrie
Droites et plans de l'espace
Droites dans l'espace
Deux droites sont dites coplanaires s'il existe un plan auquel elles appartiennent toutes les deux
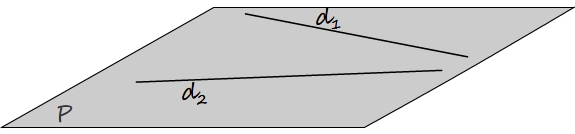
Les droites d1 et d2 appartiennent toutes au même plan (P) elles sont donc coplanaires
Deux droites de l'espace sont parallèles à condtion d'être coplanaires et de n'avoir aucun point commun
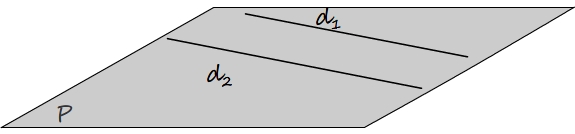
Les droites d1 et d2 sont parallèles
Si deux droites coplanaires ne sont pas parallèles alors elles sont sécantes et possèdent un point commun.
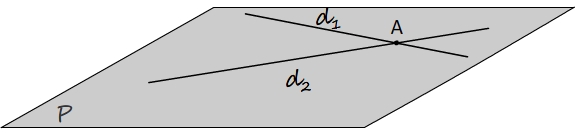
Les droites d1 et d2 sont sécantes au point A
Remarques:
- Si deux droites ne sont pas coplanaires alors elles ne sont ni parallèles ni sécantes
- Si deux droites parallèles possèdent un point commun alors elles sont confondues
Propriété: si deux droites sont parallèles à une même troisièmes alors elles sont parallèles entre elles.
Droites et plans
Une droite appartient à un plan si chacun des ses points appartiennent à ce plan.
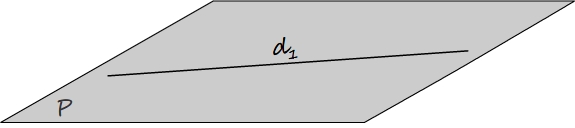
La droite d1 appartient au plan P
Pour montrer qu'une droite appartient un plan il suffit de montrer que deux points de cette droite appartient au plan.
Une droite est parallèle à un plan si elle ne possède aucun point commun avec ce plan
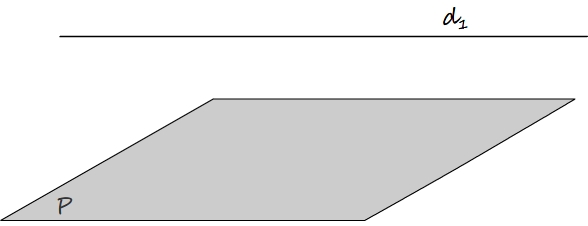
La droite d1 est parralèle au plan P
Théorème: si une droite est parallèle une droite apppartenant à un plan alors elle est aussi parallèle plan
Une droite et un plan sont sécants si ils possèdent un seul point commun avec ce plan
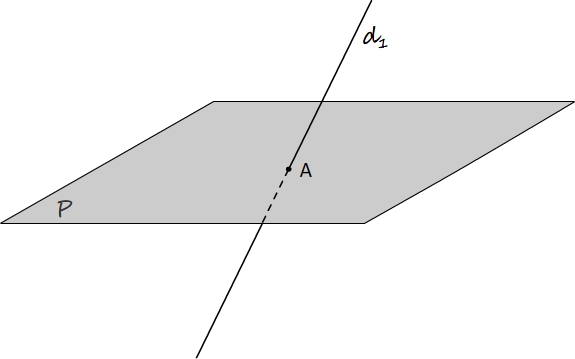
La droite d1 et le plan P sont sécants au point A
Remarque: si un une droite n'est pas parallèle à un plan elle lui est sécante, si une droite n'est pas sécante à une droite elle lui est parallèle.
Plans
Deux plans sont confondus si tous leurs points sont communs

Les plans P et P' sont confondus
Deux plans sont parallèles s'ils n'ont aucun point commun
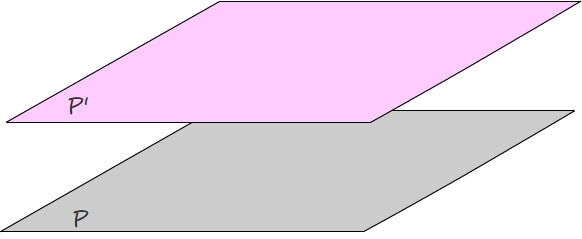
Les plans P et P' sont parallèles
Deux plans sont sécants s'ils ont au moins un point en commun
Théorème: si un plan P possède deux droites sécantes parrallèles à un plan P' alors les plans P et P' sont parallèles.
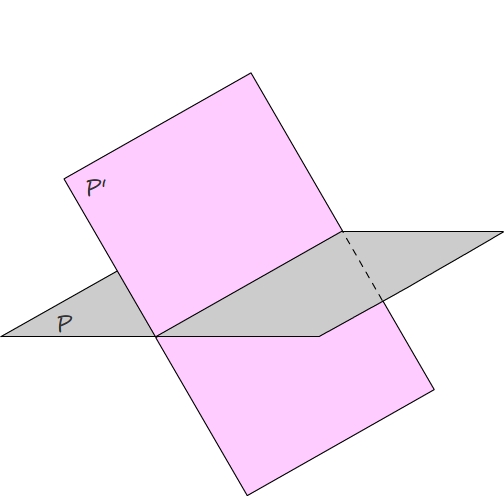
Les plans P et P' sont sécants
Si deux plans sont sécant alors leur intersection correspond à une droite
Propriété: Si une droite d est parallèle à un plan P et si d appartient à un plan P' sécant avec P alors la droite d'intersection des deux points est parallèle à d
Théorème du toit: si une droite d1 appartenant à un plan P est parallèle à une droite d2 appartenant au plan P' sécant avec P alors la droite d'intersection de ces deux plans est parallèle à d1 et d2.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
