Analyse - Cours Terminale S
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Analyse - Cours Terminale S
Analyse - Cours Terminale S
Relation fonctionnelle et propriétés algébriques
Relation fonctionnelle
soient deux réels "a" et "b" strictement positifs tels que a = exp(a') et b= exp(b') ce qui impliqe que a' = ln(a) et b' = ln(b)
Ln (a.b) = ln (exp(a').exp(b'))
= ln ( exp(a'+b'))
= a' + b'
= ln(a) + ln(b)
Relation fonctionnelle pour tous réels strictement positif a et b:
Le logarithme du produit de deux nombres est donc égal à la somme du logarithme de chaque nombre
Autres relations
Soit a un réel strictement positif, il peut s'écrire sous la forme:
a = exp (ln(a))
Par conséquent pour tout entier n:
an = exp(ln(a))n
an = exp(n.ln(a))
ln (an) = ln ( exp(n.ln(a)) )
ln (an) = n.ln(a)
Pour tout réel strictement positif "a" et tout enier n:
Le logarithme néperien d'un nombre élevé à la puissance "n" correspond donc au produit de cette puissante "n" par le logarihtme népérien du nombre.
Soit "a" un réel strictement positif :
a . 1 = 1
a
ln (a . 1 ) = ln (1)
a
ln (a) + ln( 1 ) = 0
a
ln( 1 ) = - ln (a)
a
Pour tout réel strictement positif:
a
Le logarithme néperien de l'inverse d'un nombre correspond donc à l'opposé du logarithme néperien de ce nombre
Pour tous réels a et b strictement positifs:
ln( a ) = ln(a . 1 )
b b
= ln(a) + ln( 1 )
b
= ln(a) - ln(b)
pour tous réels a et b strictement positifs:
b
Le logarithme néperien du rapport de deux nombres correspond donc à la différence des logarithmes de chacun de ces nombres.
Pour tout réel "a" strictement positif:
ln (a) = ln (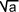 2)
2)
= 2 ln(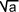 )
)
donc ln(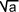 ) = 1 ln(a)
) = 1 ln(a)
2
Pour tout réel strictement positif:
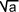 ) = 1 ln(a)
) = 1 ln(a) 2
Le logarithme népérien de la racine carrée d'un nombre correspond donc à la moitié du logaritme néperien de ce nombre.
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
