Les fonctions - Classe de seconde

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Les fonctions - cours de seconde

Fonctions de réference

La fonction carré

Définition

La fonction carrée est définie par la formule f(x) = x²
L'image d'un nombre par cette fonction correspond au carré de ce nombre
Exemples:
f(0) = 0²
      = 0
f(1) = 1²
       = 1
f(2) = 2²
       = 4
f(3) = 3²
       = 9
f(-4) = (-4)²
        = 16

Ensemble de définition

La fonction carrée est définie sur l'ensemble des nombres réels

Courbe représentative

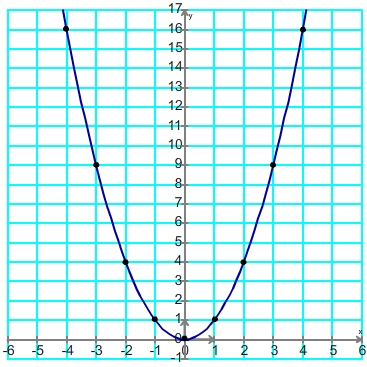
La fonction carrée est représentée par une courbe appelée "parabole". Cette courbe est symétrique par rapport l'axe des ordonnée, elle est orientée vers le haut et comporte un point particulier appelé "sommet" situé sur l'axe de symétrie et correspondant aussi à un minimum de la fonction. Le sommet à pour coordonnées (0 ; 0) et coïncide avec l'origine du repère.
Pour tracer la courbe représentative de la fonction carrée on complète d'abord un tableau de valeurs, on peut se contenter de chercher l'images des points positifs puis d'ajouter leurs opposés sachant que leur image est la même.

x	-4	-3	-2	-1	0	1	2	3	4
f(x)	16	9	4	1	0	1	4	9	16

 

Antécédent d'un nombre

- Les nombres réels négatifs ne possèdent pas d'antécédent puisque le carrée d'un nombre réel est toujours positif (quelque soit x, f(x) > 0)
- Le nombre 0 possède un seul antécédent qui est le nombre 0 car f(0) = 0 (0² = 0)
- Chaque nombre réel positif possède deux antécédents qui sont les opposés l'un de l'autre. En effet si y₁ est un nombre réel positif son antécédent x₁ est tel que:
f(x₁) = y₁
x₁² = y₁
x₁ =   ou x1 = -
Un nombre réel positif y1 possède donc par la fonction carrée les antécedents et -

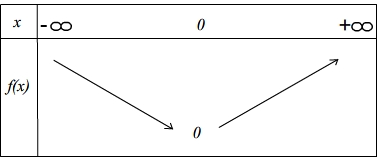
Variations

La fonction carrée est décroissante sur l'intervalle des réels négatifs puis croissante sur l'intervalle des réels positifs.

Signe

Le carré d'un nombre étant toujours positif par conséquent la fonction carrée est positive sur la totalité de son ensemble de définition: quelque soit x f(x)0