Les fonctions - Classe de seconde

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Les fonctions - cours de seconde

Fonctions de réference

fonction inverse

Définition

Comme son nom l'indique, la fonction inverse associe à chaque nombre de son ensemble de définition une image qui correspond à l'inverse de ce nombre, elle est définie par la formule:
f(x) =  1  
           x

Ensemble de définition

La division est possible par tout nomber réel sauf pour zéro qui est exclu de l'ensemble de définition de la fonction inverse. La fonction inverse est donc définie sur l'inervalle ] ; 0[ U ]0 ; [ que l'on peut également noté R -{0} ou R*

Courbe représentative

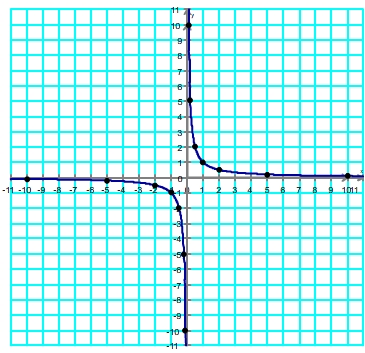
La fonction inverse est représentée par une courbe appelée hyperbole qui est symétrique par rapport à l'origine du repère c'est à dire le point O de coordonées ( 0 ; 0 ). Cette symétrie implique que si un point (x₁ ; y₁) appartient à la courbe alors le point (-x₁ ; -y₁)  lui appartient aussi. Les variations de la fonction sont plus importantes à proximité de l'origine, par conséquent son tableau de de valeurs doit comporter davantages de points dans cette zone.

Antécédent

Tous les nombres de l'ensemble des réels possèdent un seul et unique antécédent par la fonction inverse à l'exception de zéro qui n'en possède aucun.

Si l'on recherche l'antécédent x₁ d'un nombre y₁ alors:
f(x₁) = y₁
  1   =  y₁
 x₁ 
x₁ =  1  
        y₁
L'antécédent d'un nombre y1 est donc son inverse  1  
                                                                                  y₁

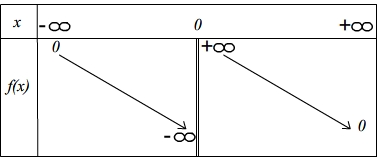
Variations

La fonction inverse est décroissante sur l'intervalle ] ; 0[ puis sur l'intervalle ] 0 ; [ mais on ne peut pas considérer qu'elle est décroissante sur la totalité de son ensemble de définition en raison de la discontinuité qui existe entre les deux parties de ce dernier et qui implique que pour tout x₁ appartenant à ]- ; 0[ et tout x₂ appartenant à ] 0 ;  [  alors f(x₁)  < f(x₂) (car f(x₁) est négatif et f(x₂) est positif).

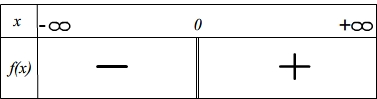
Signe

La fonction inverse est negative sur ]- ; 0[ et positive sur  ] 0 ; +inf [