Les fonctions - Classe de seconde
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Les fonctions - cours de seconde
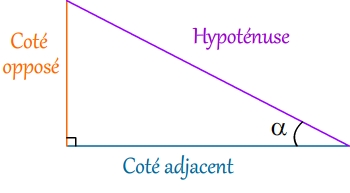
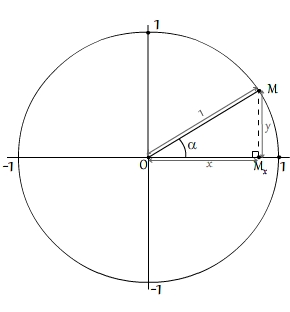
Trigonométrie
Cosinus et Sinus
|
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :