Les fonctions - Classe de seconde

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Les fonctions - cours de seconde

Inéquations

Résolution graphique d'inéquations

Lorsque la résolution algébrique d'une inéquation n'est pas possible, on peut essayer une résolution graphique fournissant des solutions entâchées d'incertitude (la lecture de valeurs sur un graphique s'accompagne toujour d'une certaine imprécision) mais applicable quelle que soit la complexité des expressions. Résolution d'une inéquation de type f(x) a ou f(x)a La résolution de ce type d'inéquation a déjà été présenté dans la fiche "résoudre graphiquement une inéquation" dans le chapitre sur l'étude qualitative des fonctions. En résumé il suffit, sur le graphique où figure la courbe de la fonction f, de tracer la courbe d'équation y = a, de repérer les points d'intersection entre la courbe et la droite. Les intervalles d'abscisses limités par ces points correspondent aux solutions. Remarques: - Résoudre une inéquation de type f(x)0 revient à determiner l'ensemble des abscisses pour lesquels la courbe est au dessus de l'axe des abscisses. - Résoudre une inéquation de type f(x)0 revient à determiner l'ensemble des abscisses pour lesquels la courbe est en dessous de l'axe des abscisses.   Résolution d'une équation de type f(x)  g(x) Dans ce cas il est nécessaire de disposer sur un même graphique des courbes représentatives des fonctions g et f. La démarche est ensuite comparable à celle suivie pour résoudre une équation de type f(x) a Etape 1 Repérer les points d'intersection entre les deux courbes Repérage des points d'intersection 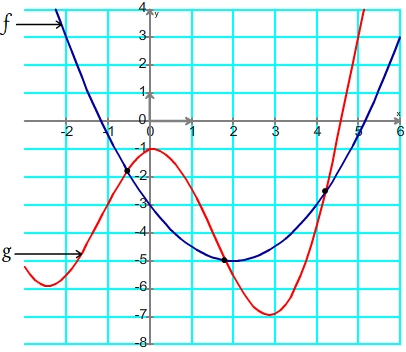Etape 2 Déterminer l'abscisse des point précédent Abscisses des points d'intersection 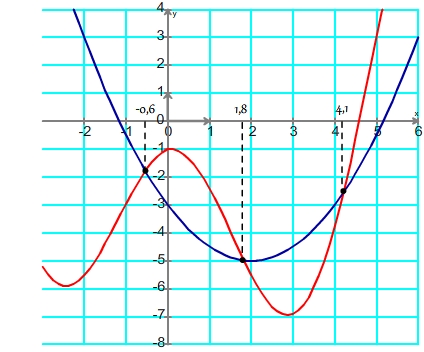Etape 3 Repérer les intervalles d'abscisses pour lesquelles la courbe de f est située au dessus de celle de g. Ces intervalles sont les solutions de l'inéquation. Repérage des intervalles de solutions 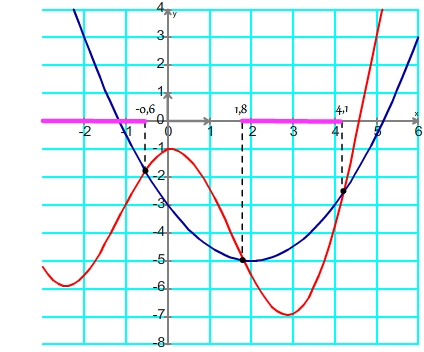Dans cet exemple, si les deux courbes sont définies sur [-3;6] alors les solutions de l'inéquation f(x)  g(x) correspondent à [-3;-0,6] U [1,8;4,1] Résolution d'une équation de type f(x)  g(x) Etape 1 Repérer les points d'intersection entre les deux courbes Repérage des points d'intersection Etape 2 Déterminer l'abscisse des point précédent Abscisses des points d'intersection Etape 3 Repérer les intervalles d'abscisses pour lesquelles la courbe de f est située en dessous de celle de g. Ces intervalles sont les solutions de l'inéquation. Repérage des intervalles de solutions 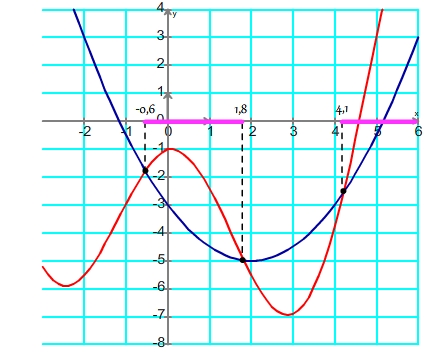Dans cet exemple, si les deux courbes sont définies sur [-3;6] alors les solutions de l'inéquation f(x)  g(x) correspondent à [-0,6;1,8] U [4,1;6]