Les fonctions - Classe de seconde
Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir
Les fonctions - cours de seconde
Etudes de fonctions
Fonctions polynôme de degré 2
Les polynomes Une fonction polymone de degré "n" s'exprime comme une somme de termes qui sont des constantes réelles et des multiples de la variable x dont la puissance va de 1 jusqu'à "n". Sa formule est donc de la forme f(x) = axn +... + gx3 + hx2 + ix + j Forme développée d'un polynome de degré 2 Une fonction polynome de degré 2 possède une formule de type f(x) = ax2 + bx + c où: - "a", "b" et "c" sont des constantes réelles positives ou négatives - "a" en non nul car sinon la formule devient f(x) = bx + c et ne correspond plus à un polynome de second degré mais à une fonction affine. Forme canonique Toute fonction polynome de second degré peut s'écrire sous une forme dite "canonique" de type: f(x) = a(x-α)2 + β α correspond au nombre pour lequel la fonction atteint un extrémum (maximum ou minimum) et β correspond à la valeur de cette extremum ( β = f(α) ). (α,β) correspond aux coordonnées du sommet de la courbe qui représente la fonction polynôme de second degré. Trouver la forme canonique Pour déterminer la forme canonique il suffit de trouver α et β Méthode 1 Si l'on connait la valeur de x pour laquelle la fonction atteint un extremum (grâce au tableau de variation ou à la courbe) alors on peut en déduire directement α et β: α correspond à la valeur de "x" pour laquelle l'extremum est atteint et β = f(α) Methode 2 Si l'on développe la forme canonique on obtient: a(x-α)2 + β = a(x2 -2αx +α2) + β = ax2 -2αax + aα2+ β Si l'on compare à la forme developpée f(x) = ax2 + bx + c alors on en tire que: 2αa = b soit α = b 2a aα2 + β = c a( b )2 + β = c 2a b2 + β = c soit β = c - b2 4a 4a Ces expressions de α et β permettent de déterminer la forme canonique à partir de la forme développée. Methode 3 Si l'on connait les deux antécédents (x1 et x2) d'un nombre y1 alors l'extremum de la fonction est atteint pour le nombre correspondant à leur moyenne (en raison de la symétrie de la fonction polynôme), on en déduit que: α = x1 + x2 2 β est ensuite obtenu comme image de α: β = f(α) Cette méthode implique de pouvoir trouver les deux antécédents d'un nombre, les antécédents les plus simples à déterminer à partir de la formule développée sont ceux du nombre c. ax2 + bx +c = c ax2 + bx = 0 x(ax+b) = 0 On aboutit à une équation produit qui admet deux solutions: soit x = 0 soit (ax + b) = 0 donc x = b a Les deux antécdents du nombre c sont donc 0 et -b a D'après ce qui précède on peut en déduire que : α = (0 + -b)/2 a α = -b 2a β est alors de nouveau obtenu comme image de α: β = f(α) β = f(-b ) 2a Forme factorisée Lorsque la fonction s'annule en deux points (c'est à dire si elle ne garde pas le même signe sur la totalité de son ensemble de définition) il est possible de l'écrire sous une forme factorisée de type: f(x) = a(x-x1)(x-x2) Dans cette formule x1 et x2 sont les abscisses des points pour lesquelles la fonction s'annule, on peut le vérifier: * f(x1) = a(x1-x1)(x-x2) = a.0.(x-x2) = 0 * f(x2) = a(x-x1)(x2-x2) = a.(x-x1).0 = 0 Pour trouver la forme factorisée il suffit de connaître les antécédents de zéro, ils peuvent difficilement être obtenus à partir de la forme développée mais on peut les déterminer à partir de la forme canonique: a(x-α)2 + β = 0 a(x-α)2 = - β (x-α)2 = - β a x-α =  ou x-α = -x1 = α + ou x2 = α - L'ensemble de définition Une fonction polynome du second degré est définie sur la totalité de l'ensemble des nombres réels. La courbe représentative Cette courbe est une parabole, elle admet un axe de symétrie vertical. Elle est caractérisée par son sommet, seul point situé sur son axe de symétrie, qui correspond à une extremum de la fonction: - Si le terme "a" de la forme développée est positif alors la parabole est orientée vers le haut et le sommet correspond à un minimum. - Si le terme "a" est négatif alors la parabole est orientée vers le bas et le sommet correspond à un maximum. Avant d'établir un tableau de valeurs qui permettent de tracer la courbe il est important de déterminer les coordonnées du sommet sur lequel sera sera centré ce tableau. Il existe plusieurs méthode pour trouver ce sommet: - La forme canonique (f(x) = a(x-α)2 + β ) fait directement intervenir ses coordonnées, α est sont abscisse et β son ordonnée donc S( α ; β ) - En résolvant l'équation ax2 + bx + c = c on trouve facilement deux valeurs qui sont les antécédents du nombre "c" (voir paragraphe "Trouver la forme canonique", méthode 3). La moyenne de ces antécédents permet de trouver l'abscisse de l'axe de symétrie et du sommet de la parabole puis il suffit ensuite de calculer l'image de ce nombre pour obtenir l'ordonnée du sommet. - La forme factorisée ( f(x) = a(x-x1)(x-x2) ) fait intervenir les nombre x1 et x2 pour lesquels la fonction est nulle, ce sont donc les antécédents du nombre zéro, ils peuvent être utilisé pour trouver l'absccisse du sommet qui correspond à leur moyenne: α = (x1 + x2)/2. L'ordonnée est ensuite obenue comme image de α. Aspect génerale de la courbe
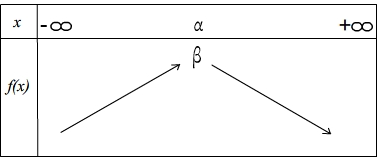
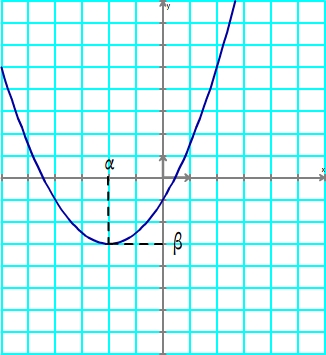 Variations Si "a" est positif, la f est décroissante sur ]  ; α ] puis croissante sur [ α ;  [Courbe Tableau de variation
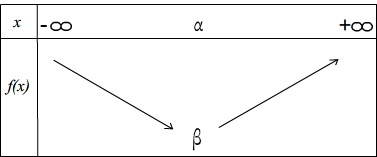
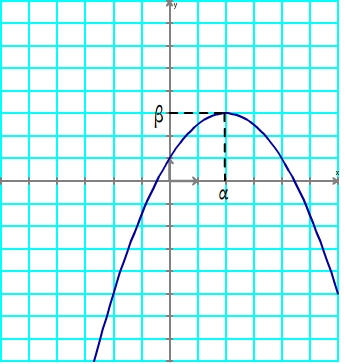
Si "a" est négatif la f est croissante sur ] ; α ] puis décroissante sur [ α ; [Courbe Tableau de variation
Signe Si a > 0 et c >0 alors la fontion est positive sur la totalité de son ensemble de variation Si a < 0 et c <0 alors la fontion est négative sur la totalité de son ensemble de variation Si a > 0 et c <0 alors f est positive sur ] ; x1 ] et [ x2 ; [, elle est négative sur [x1 ; x2]Si a < 0 et x >0 alors f est négative sur ] ; x1 ] et [ x2 ;[, elle est positive sur [x1 ; x2] |
Pour accéder à la suite du cours et participer aux amélorations inscrivez-vous :
