Les fonctions - Classe de seconde

Des cours gratuits de mathématiques de niveau lycée pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Les fonctions - cours de seconde

Chapitre 1: Les fonctions

Notion de fonction: définitions, notations et vocabulaire

Qu'est ce qu'une fonction ?

D'une manière générale une fonction permet de faire correspondre à tout élément d'un ensemble de départ un élément appartenant à un autre ensemble (l'ensemble d'arrivée).

Le plus souvent (ce sera le cas en seconde et dans les autres classes de lycée) une fonction associe chaque nombre  réel de son ensemble de définition à un autre de l'ensemble des nombred réels .
Remarque: il est possible de définir des fonctions faisant appel à plusieurs variables qui associent des couples de nombres (voire des triplets ou plus) à un nombre réel mais ce cas n'est pas étudié en classe de seconde.  

Les notations

- La plupart des fonctions sont notées à l'aide de la lettre f (f comme fonction !) ou des lettres suivantes (g, h, ....) en minuscule le plus souvent mais aussi parfois en majuscule.
- La variable qui désigne un nombre de l'ensemble de définition est en général notée "x" mais lorsque la fonction traduit la relation entre des grandeurs physiques il est courant de remplacer "x" par la lettre associée à la variable physique (t pour le temps, T pour une température, d pour une distance, v pour une vitesse etc). 
Remarque: "x" est aussi de la notation utilisée pour désigner une inconnue dans une équation et il se trouve que la notion de fonction peut être particulièrement utile pour la résolution d'équations ou d'inéquations.
- Le nombre associé par la fonction f à un nombre x de son ensemble de définition est noté f(x) ou y. Par exemple l'image du nombre 10 par une fonction f est noté f(10)

Vocabulaire

L'image: L'image (notée f(x)) d'un nombre x par une fonction f correspond au nombre associé par la fonction f à un nombre x.
Le domaine de définition: L'ensemble de définition (ou domaine de définition) d'une fonction correspond l'ensemble des nombres réels  auxquels cette fonction associe une image.
L'antécédent: Les antécédents d'un nombre "y" correspondent aux nombres de l'ensemble de définition de la fonction qui ont comme image "y". En d'autres termes, il s'agit de tous les "x" tels que f(x) = y. 

Définir une fonction

Il existe quatre manières de définir une fonction:
- Par une phrase (limité en génral à des cas simples)
- Par une formule (cas le plus fréquent et le plus facilement exploitable)
- Par un graphique (possède l'inconvénient de rendre difficile et approximative la détermination des coordonnées mais possède l'avantage de donner rapidement  une vue d'ensemble des variation et parfois de la nature de la fonction)
- Par un tableau de valeurs (Particulièrement adapté lorsque l'ensemble de définition comporte un nombre limité d'éléments)
Exemple d'une fonction même fonction f définie de 4 manières différentes:
- Phrase: f associe à tout nombre x réel un nombre qui lui est deux fois supérieur
- Formule: f(x) = 2 x
- Graphique

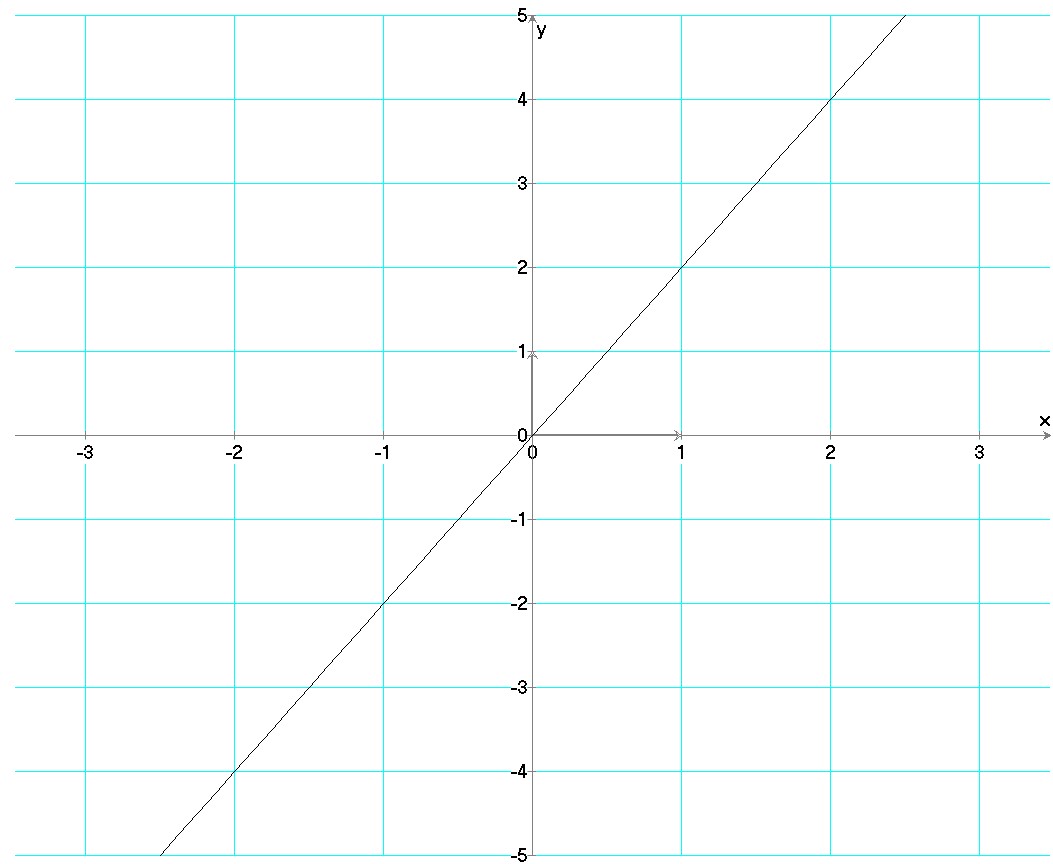
- Tableau de valeurs

x	-2	-1	0	1	2	3
f(x)	-4	-2	0	2	4	6

Reconnaître une fonction
Les fonctions ne sont pas les seules relations qu'il est possible d'établir entre des ensembles de nombres réels néanmoins ces dernières possèdent une caractéristique qui permet de les distinguer: chaque point de l'ensemble de définition ne possède qu'une seule et unique image (ce qui n'empêche pas chaque image de pouvoir posséder plusieurs antécédent).
Quelque exemples pour lesquelles des phrase, des tableaux de valeurs et des graphiques ne définissent pas une fonction:
 - Phrase: à chaque nombre réel x on associe son carré et son cube. Il ne s'agit pas d'une fonction car car chaque réel (sauf 0 et 1) possède deux images.
- Tableau de valeur 

x	-2	-1	0	- 2	-3	-4
f(x)	4	3	0	8	9	12

Dans ce cas f ne définit pas une fonction car le point x=-2 possède deux images (4 et 8).
- Graphique

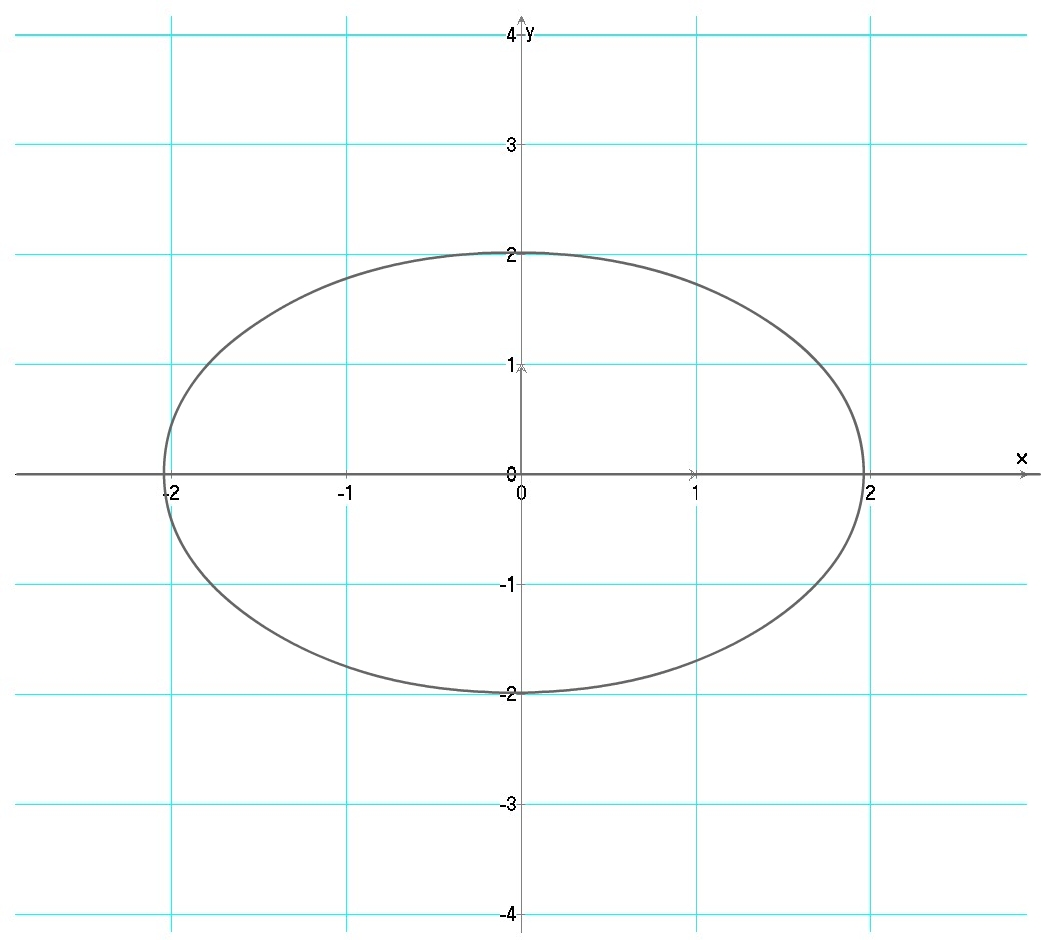
Cette graphique ne permet pas de définir une fonction car la plupart des abscisses sont associées à deux points. Par exemple le point d'abscisse 0 est associé au point (0 ; 2) mais aussi au point (0 ; -2)